 por ubelima » Sáb Abr 28, 2012 09:39
por ubelima » Sáb Abr 28, 2012 09:39
Ola, estou com dificuldade em determinar a area de um triangulo. a questão apresentam um triângulo ABC com seus pontos medios M(0,1,3), N(3,-2,2) e P(1,0,2).
Desenhei o triangulo, relacionei os dados com diversa formulas, mas sem sucesso.
Se alguem puder me orientar, agradeço o apoio.
-
ubelima
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Abr 28, 2012 09:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Guill » Sáb Abr 28, 2012 10:05
por Guill » Sáb Abr 28, 2012 10:05
Primeiramente, sabemos que o triângulo ABC é compostro por três lados, AB, BC e AC. Sabemos também que a área de um triângulo é a metade do produto da base pela altura.
Uma vez que temos os pontos médios dos lados como:
M = (0 ; 1 ; 3) ---> Ponto médio de AB
N = (3 ; -2 ; 2) ---> Ponto médio de AC
P = (1 ; 0 ; 2) ---> Ponto médio de BC
Suponhamos os vetores A, B e C tais que:
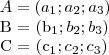
Fica claro que:

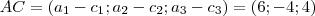

Resolvendo o sistema por igualdade de vetores, encontraremos todos os valores dos vetores. Depois disso, basta calcular o comprimento de cada um dos lados desse triângulo e usar a relação:
![Área = \sqrt[]{p(p-a)(p-b)(p-c)} Área = \sqrt[]{p(p-a)(p-b)(p-c)}](/latexrender/pictures/cc2eaa97c020b4f32cf2f1844f999792.png)
Onde p é o semiperímetro e a, b e c são os lados do triâgulo.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo de área (produto vetorial)
por wlima » Sáb Abr 28, 2012 00:45
- 2 Respostas
- 12572 Exibições
- Última mensagem por wlima

Sáb Abr 28, 2012 09:02
Geometria Analítica
-
- [calculo vetorial e geometria analitica] produto escalar
por eulercx » Sáb Nov 07, 2015 16:57
- 0 Respostas
- 2512 Exibições
- Última mensagem por eulercx

Sáb Nov 07, 2015 16:57
Geometria Analítica
-
- produto escalar calculo vetorial e geometria analitica.
por eulercx » Sáb Nov 07, 2015 16:55
- 0 Respostas
- 2275 Exibições
- Última mensagem por eulercx

Sáb Nov 07, 2015 16:55
Geometria Analítica
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4948 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Produto Vetorial
por ARCS » Sex Mai 20, 2011 08:59
- 1 Respostas
- 2364 Exibições
- Última mensagem por LuizAquino

Sex Mai 20, 2011 10:25
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


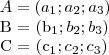

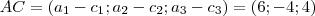

![Área = \sqrt[]{p(p-a)(p-b)(p-c)} Área = \sqrt[]{p(p-a)(p-b)(p-c)}](/latexrender/pictures/cc2eaa97c020b4f32cf2f1844f999792.png)
