 por bira19 » Seg Fev 20, 2012 07:24
por bira19 » Seg Fev 20, 2012 07:24
-4x+24x-y-32=0
O que completar o quadrado na variavel adequada ?
como encontrar equação canonica desta parabola ?
como identificar o vertice ?
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
 por MarceloFantini » Seg Fev 20, 2012 08:49
por MarceloFantini » Seg Fev 20, 2012 08:49
Se a sua equação for

isto não é uma parábola. Por favor revise.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por bira19 » Seg Fev 20, 2012 09:35
por bira19 » Seg Fev 20, 2012 09:35
MarceloFantini escreveu:Se a sua equação for

isto não é uma parábola. Por favor revise.
A equação estava errada, a correta é esta abaixo
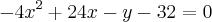
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
 por LuizAquino » Seg Fev 20, 2012 11:04
por LuizAquino » Seg Fev 20, 2012 11:04
bira19 escreveu:A equação estava errada, a correta é esta abaixo

bira19 escreveu:O que completar o quadrado na variavel adequada?
como encontrar equação canonica desta parabola ?
como identificar o vertice?
Primeiro, coloque -4 em evidência:
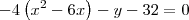
Agora, complete quadrados:
![-4\left[(x-3)^2 - 9\right] - y - 32=0 -4\left[(x-3)^2 - 9\right] - y - 32=0](/latexrender/pictures/b6deefacb1188fccc2288f878411639e.png)
Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por bira19 » Seg Fev 20, 2012 15:36
por bira19 » Seg Fev 20, 2012 15:36
Eu não entendi o que é completar os quadrados
-
bira19
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 03, 2011 20:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletronica
- Andamento: formado
 por MarceloFantini » Ter Fev 21, 2012 12:09
por MarceloFantini » Ter Fev 21, 2012 12:09
Lembra-se da expressão
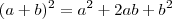
? Completar quadrados é quando você tem
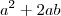
e você quer escrever como
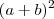
, daí lembrando que
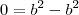
teremos
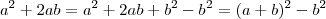
.
No caso do exercício, temos
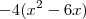
, usando o que acabei de dizer teremos
![-4(x^2 -6x +9 -9) = -4[(x-3)^2 -9] -4(x^2 -6x +9 -9) = -4[(x-3)^2 -9]](/latexrender/pictures/418a31a7b9704758c349a8b4e1c7d960.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2849 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- [Parábola] Encontrando o ponto na parábola
por Ana_Rodrigues » Ter Nov 22, 2011 20:44
- 1 Respostas
- 5000 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 21:38
Geometria Analítica
-
- Parábola
por flavio2010 » Sáb Jul 17, 2010 19:11
- 1 Respostas
- 2024 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:20
Funções
-
- Parábola
por flavio2010 » Dom Jul 18, 2010 19:42
- 1 Respostas
- 1915 Exibições
- Última mensagem por Tom

Dom Jul 18, 2010 23:31
Funções
-
- Parábola
por flavio2010 » Sex Jul 23, 2010 19:16
- 1 Respostas
- 2017 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 24, 2010 01:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




isto não é uma parábola. Por favor revise.
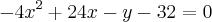

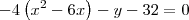
![-4\left[(x-3)^2 - 9\right] - y - 32=0 -4\left[(x-3)^2 - 9\right] - y - 32=0](/latexrender/pictures/b6deefacb1188fccc2288f878411639e.png)


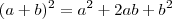 ? Completar quadrados é quando você tem
? Completar quadrados é quando você tem 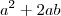 e você quer escrever como
e você quer escrever como 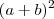 , daí lembrando que
, daí lembrando que 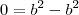 teremos
teremos 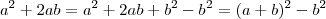 .
. 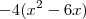 , usando o que acabei de dizer teremos
, usando o que acabei de dizer teremos ![-4(x^2 -6x +9 -9) = -4[(x-3)^2 -9] -4(x^2 -6x +9 -9) = -4[(x-3)^2 -9]](/latexrender/pictures/418a31a7b9704758c349a8b4e1c7d960.png) .
.
