Se você iguala as duas equações você vai ficar com uma equação e duas incógnitas ( y e b ) e vai ter que parametrizar a solução já que o problema admite infinitas soluções, isto é, existem infinitas retas

que satisfazem a condição de ser paralela à reta

e distinta dela.
Para determinar um b que satisfação as condições do problema, pode-se fazer o seguinte:
Reescrevemos as equações de

e

isolando o

:
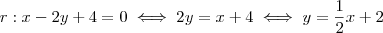

Obtivemos assim as equações reduzidas (
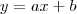
onde

representa o coeficiente angular da reta e

indica o valor de y quando a reta intersecta o eixo vertical ) das retas.
Duas retas para serem paralelas devem possuir o mesmo coeficiente angular. Para serem distintas devem possuir o termo independente de x diferentes entre si.
No caso da reta

o termo independente é 2, essa reta corta o eixo vertical em

. Já a reta

corta o eixo vertical em

. Assim basta que ambas tenham o mesmo coeficiente angular para que sejam paralelas e distintas, isto é:

Agora é com você.


 que satisfazem a condição de ser paralela à reta
que satisfazem a condição de ser paralela à reta  e distinta dela.
e distinta dela. :
: 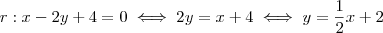

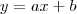 onde
onde  representa o coeficiente angular da reta e
representa o coeficiente angular da reta e  indica o valor de y quando a reta intersecta o eixo vertical ) das retas.
indica o valor de y quando a reta intersecta o eixo vertical ) das retas. . Já a reta
. Já a reta  . Assim basta que ambas tenham o mesmo coeficiente angular para que sejam paralelas e distintas, isto é:
. Assim basta que ambas tenham o mesmo coeficiente angular para que sejam paralelas e distintas, isto é:


 .
.
 :
: