é, de fato. minha ultima pergunta estava incoerente...
eu fui tentar resolver na lousa, com tempo e eu até consegui... mas foi quaaase que trapaceando...
Precisei desenhar a circunferencia e a reta para dai ter uma epifania quanto à posição da elipse.
Voce disse que ja desenhou... deve ter percebido que pra desenhar uma elipse que tangencia internamente uma circunferencia voce percebe que o eixo maior da elipse é o diametro da circunferencia. O problema é quanto à posição da elipse, no eixo Ox ou no Oy ?
Se voce desenhar a reta e a circunferencia, percebe que como a reta "corta" o eixo Ox "dentro" da circunferencia é impossivel colocar uma elipse lá dentro tangenciando a reta. Eu fiz essa obsercação baseada no seguinte desenho :

Uploaded with
ImageShack.usperceba que é impossivel colocar uma elipse com o eixo maior contido no Ox de forma a tangenciar a circunferencia internamente E a reta.
Mas no eixo Oy é possivel.
Utilizando essas observações sei que o eixo maior está no y e sei que
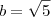
pois o eixo maior é na verdade o diametro da circunferencia.
minha elipse fica então da forma:
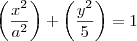
mas ela ainda depende de "a". é preciso usar a informação de que a elipse tangencia a reta.
isolando o y na equação da reta, temos:
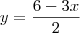
correto?
Dizer que a elipse tangencia a reta, é também dizer que existe UM ponto, apenas UM, que resolve a equação da elipse e da reta ao mesmo tempo.
Caso existam 2 pontos a reta está cortando a elipse.
Então o que eu fiz foi substituir esse Y da reta na equação da elipse, e determinar "para qual 'a'" existe apenas um valor de x que resolve a equação...
OFF: Perceba que o exercicio foi ficando cada vez mais absurdo, mais dificil, e mais cabuloso. Eu tenho certeza que deve existir algum jeito mais simples...Aliás, utilizando calculo diferencial e integral esse exercicio se resolve bem facilmente, caso voce saiba calculo eu posso dizer o que faria.
a equação fica

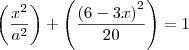

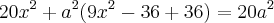
quando voce faz a distributiva e tudo mais, isso vai virar uma equação de segundo grau em X.
Voce quer que Delta de zero para que só exista uma raiz e não duas (hipotese da tangencia).
igualando o delta a zero voce deve descobrir o A que corresponde a tangencia.
com isso voce chega a descobrir o ponto P, ele vai ser a raiz dessa equação.
OFF: Esse exercicio ficou MUUUUUUUUUUITO mais complicado do que eu esperava... Desculpe se eu confundi mais ainda, ou se eu não ajudei em nada, mas ficou tão grande que era impossivel evitar contas assim...... Talvez o meu erro tenha sido pensar antes em descobrir a equação da elipse...
De qualquer forma desculpe se eu compliquei.
Espero que outra pessoa possa resolver também de maneira mais simples...
Espero ter sido de alguma ajuda. obrigado.

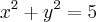 e que a reta de equaçao 3x+2y=6 é tangente á elipse no ponto P.determine as coordenadas de P.
e que a reta de equaçao 3x+2y=6 é tangente á elipse no ponto P.determine as coordenadas de P.

 centrada no ponto
centrada no ponto  ...
...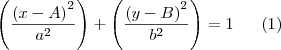


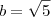 pois o eixo maior é na verdade o diametro da circunferencia.
pois o eixo maior é na verdade o diametro da circunferencia. 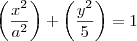
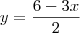

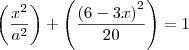

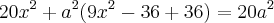

 .
.



