1°) Adicionando a medida do complemento de um ângulo ao suplemento do mesmo ângulo, obteremos um Ângulo obtuso igual a 130°. qual seria esse ângulo ?
2°) Determine o valor do triplo de x na figura abaixo.

Uploaded with ImageShack.us



Lucasss escreveu:Não sei se está na área correta...
Lucasss escreveu:1°) Adicionando a medida do complemento de um ângulo ao suplemento do mesmo ângulo, obteremos um Ângulo obtuso igual a 130°. qual seria esse ângulo ?




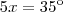
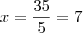
 Uma dica para você: Faça mais exercícios de equação, pois sem isso, você não conseguirá resolver problemas deste tipo.
Uma dica para você: Faça mais exercícios de equação, pois sem isso, você não conseguirá resolver problemas deste tipo.
1°) Adicionando a medida do complemento de um ângulo ao suplemento do mesmo ângulo, obteremos um Ângulo obtuso igual a 130°. qual seria esse ângulo ?
(90° - a) + (180° - a) = 130°

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante