 por -civil- » Qua Jun 15, 2011 21:05
por -civil- » Qua Jun 15, 2011 21:05
Mostre que os pontos A = (-2, 0, 1), B = (0, 0, -1), C = (1, 1, 1), D = (-2,-1,-2) e E = (1, 2, 2) são vértices de uma pirâmide e calcule seu volume.
A minha ideia era encontrar a base da pirâmide, encontrar a altura (encontrando o plano em que a base está contida, e usando a fórmula de distância entre o plano e o ponto que é vértice da pirâmide) e depois colocar esses valores na fórmula para calcular o volume da pirâmide.
Primeiramente, eu calculei todas as distâncias entre esses pontos. Eu encontrei que

,
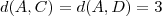
e

. Depois eu coloquei as coordenadas de todos os pontos e percebi que só daria certo se eu considerasse como base os segmentos BC, BD, AC e AD. Mas a figura formada por esses segmentos não forma um retângulo, mas um polígono meio estranho. Está certo o meu raciocínio? Existe outra forma melhor de encontrar o volume dessa pirâmide?
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qui Jun 16, 2011 00:20
por LuizAquino » Qui Jun 16, 2011 00:20
Primeiro, você tem que provar que esses vértices formam uma pirâmide. Para isso, você tem que mostrar que 4 desses pontos estão em um mesmo plano (formando um polígono) e o outro restante não.
Para encontrar esses 4 pontos, escolha 3 e verifique se apenas um dos outros dois não está no mesmo plano que eles.
Por exemplo, digamos que você escolha os pontos A, B e C. Você deve determinar o plano que os contém. Em seguida, verifique se apenas D ou apenas E não está nesse plano. Em caso negativo, você deve escolher outros 3 pontos e continuar o processo. Note que você terá ao todo 10 possibilidades de escolher 3 pontos em um conjunto de 5. Se os 10 testes falharem, então não há pirâmide com esses vértices.
Agora, suponha que esses vértices formam uma pirâmide e você achou quais são os 4 que formam a base. A partir disso você precisa determinar a área da base e a altura da pirâmide para poder calcular o volume. A altura da pirâmide você já tem a ideia de como calcular. Se você não tem ideia de como calcular a área da base, lembre-se que qualquer quadrilátero pode ser dividido em dois triângulos.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por -civil- » Sáb Jun 18, 2011 12:13
por -civil- » Sáb Jun 18, 2011 12:13
Com sua ajuda conseguir resolver. Descobri os pontos que estavam contidos no mesmo plano e calculei a área da base através da área dos dois triângulos que formam a base.
Muito obrigado!
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Volume de uma piramide hexagonal
 por joserd » Qua Jan 25, 2012 20:24
por joserd » Qua Jan 25, 2012 20:24
- 7 Respostas
- 7597 Exibições
- Última mensagem por joserd

Qua Jan 25, 2012 22:33
Cálculo: Limites, Derivadas e Integrais
-
- Volume do tronco da pirâmide
 por erikamurizinepires12 » Qui Fev 09, 2017 16:02
por erikamurizinepires12 » Qui Fev 09, 2017 16:02
- 1 Respostas
- 8263 Exibições
- Última mensagem por 314159265

Seg Fev 13, 2017 02:31
Geometria Espacial
-
- Geometria Analitica Volume da piramide
por Diego Silva » Sex Ago 02, 2013 23:39
- 1 Respostas
- 4172 Exibições
- Última mensagem por mecfael

Dom Ago 18, 2013 22:58
Geometria Analítica
-
- PAS 2011- Volume do casco da pirâmide
 por Larissa belchior » Seg Nov 30, 2015 17:08
por Larissa belchior » Seg Nov 30, 2015 17:08
- 0 Respostas
- 2901 Exibições
- Última mensagem por Larissa belchior

Seg Nov 30, 2015 17:08
Geometria Espacial
-
- >>>>>>Volume da Pirâmide de Base Hexagonal<<<<<
por futuromilitar » Sáb Mai 21, 2016 17:29
- 1 Respostas
- 6264 Exibições
- Última mensagem por futuromilitar

Qui Mai 26, 2016 22:00
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,
, 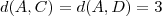 e
e  . Depois eu coloquei as coordenadas de todos os pontos e percebi que só daria certo se eu considerasse como base os segmentos BC, BD, AC e AD. Mas a figura formada por esses segmentos não forma um retângulo, mas um polígono meio estranho. Está certo o meu raciocínio? Existe outra forma melhor de encontrar o volume dessa pirâmide?
. Depois eu coloquei as coordenadas de todos os pontos e percebi que só daria certo se eu considerasse como base os segmentos BC, BD, AC e AD. Mas a figura formada por esses segmentos não forma um retângulo, mas um polígono meio estranho. Está certo o meu raciocínio? Existe outra forma melhor de encontrar o volume dessa pirâmide?




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.