 por stanley tiago » Dom Fev 13, 2011 18:35
por stanley tiago » Dom Fev 13, 2011 18:35
calcule a area de um triangulo retangulo , sabendo que um deuseus catetos mede o triplo do outro e que seu perimetro vale
![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png)
unidades
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Fev 13, 2011 21:28
por Molina » Dom Fev 13, 2011 21:28
Boa noite, Stanley.
Sejam
a,
b e
c os lados do triangulo retangulo. Se o cateto
a mede x e o cateto
b mede 3x, temos que a hipotenusa
c mede
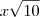
. Se o perimetro mede
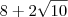
temos que:

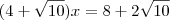
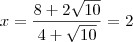
Agora você ja tem os valores dos lados do triangulo. Basta substituir na formula da area e encontrar a solucao da questao.
Qualquer duvida informe,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por stanley tiago » Seg Fev 14, 2011 19:11
por stanley tiago » Seg Fev 14, 2011 19:11
obrigado é isso mesmo , eu consegui chegar no resultado.
é que tem q desenvolver a soma dos quadrados né ?
só tirar a raiz daqui nao é permitido ?
![a=\sqrt[]{x^2+(3x)^2} a=\sqrt[]{x^2+(3x)^2}](/latexrender/pictures/5ad476d4ae6a2c0e04441df9104eeaee.png)

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Fev 14, 2011 21:54
por Molina » Seg Fev 14, 2011 21:54
stanley tiago escreveu:obrigado é isso mesmo , eu consegui chegar no resultado.
é que tem q desenvolver a soma dos quadrados né ?
só tirar a raiz daqui nao é permitido ?
![a=\sqrt[]{x^2+(3x)^2} a=\sqrt[]{x^2+(3x)^2}](/latexrender/pictures/5ad476d4ae6a2c0e04441df9104eeaee.png)

Boa noite.
Foi isso que eu fiz, veja mais detalhadamente:


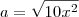
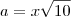

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por stanley tiago » Seg Fev 14, 2011 22:00
por stanley tiago » Seg Fev 14, 2011 22:00
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4666 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Sáb Fev 19, 2011 10:26
- 1 Respostas
- 1924 Exibições
- Última mensagem por stanley tiago

Dom Fev 20, 2011 17:48
Geometria Analítica
-
- Teorema de Pitágoras
por Lorrane12 » Sex Mar 23, 2012 19:50
- 9 Respostas
- 12647 Exibições
- Última mensagem por DanielFerreira

Sex Mar 30, 2012 00:19
Trigonometria
-
- Teorema de Pitágoras
por Luciana Dias » Sex Mar 23, 2012 22:46
- 2 Respostas
- 1993 Exibições
- Última mensagem por Luciana Dias

Sex Mar 23, 2012 23:06
Trigonometria
-
- [teorema de Pitágoras]
por Alane » Qui Ago 02, 2012 09:45
- 3 Respostas
- 2985 Exibições
- Última mensagem por Alane

Qui Ago 02, 2012 11:39
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png) unidades
unidades

![8+2\sqrt[]{10} 8+2\sqrt[]{10}](/latexrender/pictures/13d92a9cb0260070fa12e88a4b922725.png) unidades
unidades
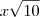 . Se o perimetro mede
. Se o perimetro mede 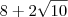 temos que:
temos que:
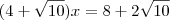
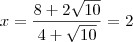


![a=\sqrt[]{x^2+(3x)^2} a=\sqrt[]{x^2+(3x)^2}](/latexrender/pictures/5ad476d4ae6a2c0e04441df9104eeaee.png)

![a=\sqrt[]{x^2+(3x)^2} a=\sqrt[]{x^2+(3x)^2}](/latexrender/pictures/5ad476d4ae6a2c0e04441df9104eeaee.png)


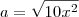
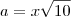



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
