 por Goldragon979 » Seg Jan 03, 2011 15:41
por Goldragon979 » Seg Jan 03, 2011 15:41
A minha dúvida é qual a diferença entre os seguintes métodos, e em que situações se deve usar cada um:
cos(a^b) = (a1xb1 + a2xb2)/(||a|| x ||b||)
e
a.b = ||a|| x ||b|| x cos do ângulo
Não sei se fui capaz de expressar correctamente a minha dúvida.
Obrigado.
-
Goldragon979
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Jan 03, 2011 15:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciências e Tecnologias
- Andamento: cursando
 por MarceloFantini » Seg Jan 03, 2011 17:37
por MarceloFantini » Seg Jan 03, 2011 17:37
São expressões equivalentes.
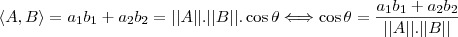
. A segunda é normalmente usada quando se quer encontrar o ângulo entre os vetores, e a primeira quando você quer encontrar o produto escalar (ou interno).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercicio Vectores
 por rmsf » Sáb Fev 02, 2013 11:32
por rmsf » Sáb Fev 02, 2013 11:32
- 1 Respostas
- 1108 Exibições
- Última mensagem por Russman

Sáb Fev 02, 2013 13:38
Álgebra Linear
-
- [Vectores] Exercicio
 por rmsf » Sáb Fev 02, 2013 14:01
por rmsf » Sáb Fev 02, 2013 14:01
- 0 Respostas
- 582 Exibições
- Última mensagem por rmsf

Sáb Fev 02, 2013 14:01
Álgebra Linear
-
- Ângulos
 por admin » Sex Set 07, 2007 06:42
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 13568 Exibições
- Última mensagem por Numwantida

Qui Mai 24, 2018 05:06
Pérolas
-
- Angulos ??????
por ByRobert » Qui Set 01, 2011 12:59
- 6 Respostas
- 9045 Exibições
- Última mensagem por LuizAquino

Qui Set 01, 2011 21:24
Trigonometria
-
- ângulos
 por Thays » Sáb Jan 14, 2012 11:59
por Thays » Sáb Jan 14, 2012 11:59
- 6 Respostas
- 4628 Exibições
- Última mensagem por Thays

Qui Jan 19, 2012 09:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


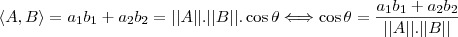 . A segunda é normalmente usada quando se quer encontrar o ângulo entre os vetores, e a primeira quando você quer encontrar o produto escalar (ou interno).
. A segunda é normalmente usada quando se quer encontrar o ângulo entre os vetores, e a primeira quando você quer encontrar o produto escalar (ou interno).


 .
.
 :
: