Gostaria de saber onde estou errando na resolução do exercício que segue. Já fiz e refiz o exercício e o meu resultado não confere com o gabarito.
--> Determine o valor de k a fim de que a equação
 tenha raízes em progressão aritmética. Em seguida, obtenha as raízes e a razão da PA.
tenha raízes em progressão aritmética. Em seguida, obtenha as raízes e a razão da PA.Estou resolvendo assim: Raízes -->
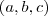 Como estão em PA:
Como estão em PA:  Logo,
Logo, 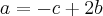 I
IQuanto a somas das raízes:
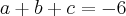 II
IIQuanto a soma dos produtos das raízes tomadas duas a duas:
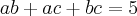 III
IIIQuanto ao produto das raízes:
 IV
IVResolvendo I --> II: Estou encontrando

Sabendo dessa raiz, estou aplicando o algoritmo de Briot-Ruffini, onde estou encontrando

Aqui que está acontecendo a divergência das respostas, o gabarito aponta
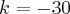 .
.Agradeço sua ajuda

Até mais.




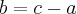 ...
...
