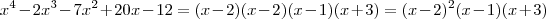Estou fazendo uma lista de exercícios só sobre simplificação e gostaria que vocês me ajudassem com uma questão particularmente difícil (pra mim).
Eu preciso simplificar a fração:
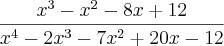
Eu tentei simplificar a do numerador (3º grau) da seguinte forma: fatorei o termo independente (no caso, o 12) e testei os resultados (positivos e negativos) na expressão pra achar uma raiz. Depois usei essa raiz no dispositivo de Briot Ruffini e cheguei a uma equação de segundo grau. O meu objetivo era encontrar as duas raizes dessa equação por "Baskaras" e com as três raizes decompor em fatores de grau 1: coeficiente do termo de maior grau .(x -
 ).(x -
).(x -  ).(x -
).(x - 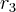 )
)O problema foi que a raiz que eu usei pra fazer Briot Ruffini foi a mesma que eu encontrei resolvendo a equação de segundo grau, ou seja, não consegui encontrar as três raizes, apenas duas. Por favor, alguém me diz os passos que eu tenho que seguir na ordem correta pra eu conseguir simplificar isso...
Na minha lista de exercícios tem umas 10 questões iguais a essa, tem até com equação de quinto grau! Se eu não consegui nem a de terceiro, que me dirá a de quarto e quinto...
Muuuuuito obrigada a quem puder me ajudar!!
Beijos!


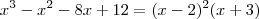
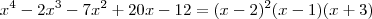

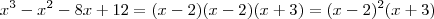
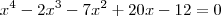 ,onde 2 é uma raiz usando Briot-Ruffini baixamos o grau e percebemos que 2 é raiz novamente, com isso ficamos com uma equação do 2 grau onde encontramos como raízes 1 e -3.
,onde 2 é uma raiz usando Briot-Ruffini baixamos o grau e percebemos que 2 é raiz novamente, com isso ficamos com uma equação do 2 grau onde encontramos como raízes 1 e -3.