 por fernandocez » Seg Mar 21, 2011 13:51
por fernandocez » Seg Mar 21, 2011 13:51
Caros amigos, venho novamente trazer mais uma questão que parecia simples e não consegui resolver. Já coloquei outras parecidas com essa. Tentei alguma coisa mas travei.
28) Sejam
a e
b números reais, tais que
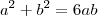
. Um valor possível para a razão

é:
resp:
![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png)
Eu tentei.
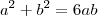
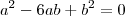
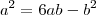
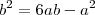
Fui até formar raízes. Será que é por ai? Aguardo uma ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Seg Mar 21, 2011 14:15
por LuizAquino » Seg Mar 21, 2011 14:15
Dicas(i) Divida toda a equação
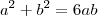
por
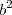
.
(ii) Faça a substituição
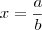
e resolva a equação do 2º grau que irá aparecer.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3544 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2490 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9256 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1818 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2663 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
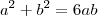 . Um valor possível para a razão
. Um valor possível para a razão  é:
é:![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png)
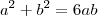
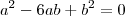
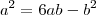
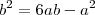

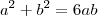 . Um valor possível para a razão
. Um valor possível para a razão  é:
é:![3+2\sqrt[]{2} 3+2\sqrt[]{2}](/latexrender/pictures/8a4f488b4902771b4ebfb90b4b32531b.png)
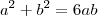
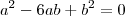
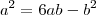
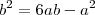

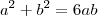 por
por 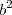 .
.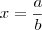 e resolva a equação do 2º grau que irá aparecer.
e resolva a equação do 2º grau que irá aparecer.
por
.
e resolva a equação do 2º grau que irá aparecer.
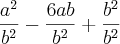
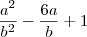
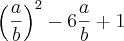
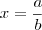
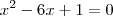
![x = 3+2\sqrt[]{2} x = 3+2\sqrt[]{2}](/latexrender/pictures/76cfdd386a5b6f2d31c9ac0ee285a6f5.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.