47. As raízes da equação x²-7x-5 = 0 são m e n. Uma equação do segundo grau cujas raízes são
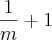 e
e 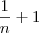 é:
é:resp: 5x²-3x-3=0
Eu fiz assim:
Tentei encontrar as raízes, delta = 69
x' =
![\frac{7+\sqrt[]{69}}{2} \frac{7+\sqrt[]{69}}{2}](/latexrender/pictures/a7cae91ca282913818f62f676df2f4a8.png)
x" =
![\frac{7-\sqrt[]{69}}{2} \frac{7-\sqrt[]{69}}{2}](/latexrender/pictures/6d49063d48d2a5a44132f9f164220d42.png)
substitui "m" por x'
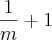
substitui "n" por x"
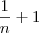
pensei que com isso encontraria as raízes da outra equação procurada, só que apareceu tanto cálculo que acho que estou no caminho errado.


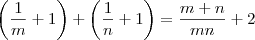 .
.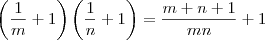 .
.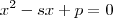 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)