A soma e o produto das raízes do polinômio P(x)= 2x²+ bx+ c são, respectivamente, -6 e 5. Assim, o valor mínimo que P(x) pode assumir pertence ao conjunto:
A) { -6 , -4 , -1 }
B) {-5 , -3 , 0 }
C) { -8 , 1 , 6 }
D) { 2 , 4 , 5 }
E) { 3 , 7 , 8 }
Resolução:
Eu resolvi aplicando Girard , que x¹ + x² = -6, logo -b/2 = -6, portanto, b = 12 e x¹.x² = 5, logo (-1)² . c/2 = 5, portanto, c = 10. assim a equação fica P(x)= 2x² + 12x + 10, tendo como raízes resolvendo a expressão -1 e -5.
Mas, não sei qual resposta certa a marca pelo o que pede a questão. Se alguém puder me ajudar, obrigado pela força !


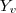 :
: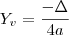



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.