 por natanaelskt » Ter Mai 14, 2013 13:45
por natanaelskt » Ter Mai 14, 2013 13:45
não consigo entender a seguinte equação.
não sei se estou errando,pois já conferi eu não consegui encontrar o erro.
267-) resolva,em complexos,a equação

sabendo que duas de suas raízes são -1 e 3.
primeiro tentei o seguinte.
a soma das raizes é r1+r2+r3+r4 = 5
o produto das raizes é r1.r2.r3.r4 = -6
sendo r1=-1 e r2= 3
substituindo na equação cheguei a r3=2 e r4= 1 (ou vice versa)
o problema é que a resposta certa é -1+i e -1-i
ajuda aew galera????
-
natanaelskt
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Seg Mar 11, 2013 15:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por carlosalesouza » Qua Mai 15, 2013 01:26
por carlosalesouza » Qua Mai 15, 2013 01:26
Na prática ela é muito simples...
É uma equação de grau 4, mas duas raízes já foram dadas... basta dividir a equação pelas raízes dadas (de preferência uma por vez) e vc vai obter uma equação de segundo grau...
Vamos à prova:
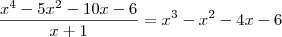
Que, por sua vez:
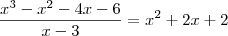
Agora, aplicando Baskhara... vamos achar o Delta:
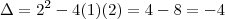
Usando complexos, a raiz de -4 é 2i
Voltando ao processo:
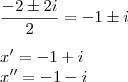
Tudo certo?
É necessário tomar cuidado com alguns problemas, pois eles vem maqueados de algo mais complexos do que realmente são...
Neste caso, vc tem uma equação de segundo grau disfarçada de equação de grau 4, num exercício que exige de vc conhecimento sobre numeros complexos, equações de segundo grau e divisão de polinômios...
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por natanaelskt » Qua Mai 15, 2013 11:06
por natanaelskt » Qua Mai 15, 2013 11:06
sim,mas eu queria saber porque o método que usei deu errado.
pode me explicar?
-
natanaelskt
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Seg Mar 11, 2013 15:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13013 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- Equação Polinomial
por Cleyson007 » Dom Jun 14, 2009 16:21
- 1 Respostas
- 5995 Exibições
- Última mensagem por Cleyson007

Qua Jun 17, 2009 09:20
Polinômios
-
- Equação Polinomial
por gustavowelp » Dom Jun 27, 2010 11:53
- 3 Respostas
- 3285 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 12:37
Sistemas de Equações
-
- Equação polinomial
por cristina » Sáb Set 18, 2010 17:29
- 5 Respostas
- 4172 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 01:45
Polinômios
-
- (ITA) Equação polinomial
por Carolziiinhaaah » Sex Fev 04, 2011 15:35
- 7 Respostas
- 5918 Exibições
- Última mensagem por Renato_RJ

Qua Fev 16, 2011 00:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 sabendo que duas de suas raízes são -1 e 3.
sabendo que duas de suas raízes são -1 e 3.

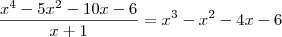
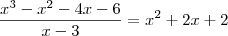
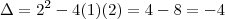
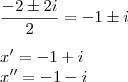



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.