 por brunadultra » Qua Jan 23, 2013 13:58
por brunadultra » Qua Jan 23, 2013 13:58
Questão 14 (UNEB-2013) Ao desmontar um cubo de Rubik (cubo mágico), uma criança percebeu que ele era formado por
vinte e sete cubinhos menores e que dentre esses existiam oito cubinhos com três faces pintadas,
doze com apenas duas faces pintadas, seis com apenas uma das faces pintadas e apenas um
cubinho não possuía nenhuma das faces pintadas.
A tabela a seguir, mostra o número de cubinhos, de cada tipo, que podem ser obtidos ao dividir
a aresta de um cubo de madeira pintado, em partes iguais.
(tabela da questão segue em anexo)
Nessas condições, pode-se afirmar que, em R, a soma dos inversos das raízes do polinômio
P(x) = P3(x) ? P1(x) + P2(x) é igual a:
Resposta: 3/5
- Anexos
-

- TABELA
-
brunadultra
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 07, 2012 23:01
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por young_jedi » Qua Jan 23, 2013 15:06
por young_jedi » Qua Jan 23, 2013 15:06
da tabela e da analise do cubo no tiramos que
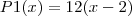

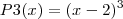
onde x é o numero de divisões das arestas do cubo
portanto

 P(x)=[(x-2)^2-12+6(x-2)](x-2)](/latexrender/pictures/8233fd5fe67f1372648e8f0e89880798.png)
encontre as raizes do polinomio e conclua, qualquer duvida comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por brunadultra » Qua Jan 23, 2013 21:18
por brunadultra » Qua Jan 23, 2013 21:18
Muito obrigada! =)
-
brunadultra
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Nov 07, 2012 23:01
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por maiarabahia » Sáb Set 07, 2013 12:50
por maiarabahia » Sáb Set 07, 2013 12:50
Olá Boa tarde, também estava com dificuldade nesta questão, mas não entendi essa parte da resolução em que
P1(x) = 12(x-2), P2... e P3... porque o x em evidencia??? Não consegui fazer essa análise.
-
maiarabahia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Set 06, 2013 12:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por young_jedi » Sáb Set 07, 2013 19:04
por young_jedi » Sáb Set 07, 2013 19:04
x é o numero de divisões das arestas então tirando as duas divisões que são dos blocos dos vértices cada aresta fica com x-2
blocos como são 12 arestas então teremos um total de 12(x-2) blocos nas arestas
já nas faces termos que em cada uma a quantidade de blocos vai ser de (x-2)² como são 6 faces então temos 6(x-2)² cubos
e no interior do cubo teremos que são (x-2)³ cubos
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [TRIGONOMETRIA] Questão UNEB 2013
 por brunadultra » Qua Jan 23, 2013 15:51
por brunadultra » Qua Jan 23, 2013 15:51
- 5 Respostas
- 10779 Exibições
- Última mensagem por zenildo

Qua Dez 13, 2017 17:28
Trigonometria
-
- [Função] Questão UNEB 2013
por brunadultra » Qua Jan 23, 2013 16:15
- 1 Respostas
- 9243 Exibições
- Última mensagem por young_jedi

Qui Jan 24, 2013 21:54
Funções
-
- [LOGARITMO] QUESTÃO UNEB 2013
por brunadultra » Qua Jan 23, 2013 18:17
- 2 Respostas
- 6326 Exibições
- Última mensagem por brunadultra

Qua Jan 23, 2013 20:47
Logaritmos
-
- [PROBABILIDADE] Questão UNEB 2013
 por brunadultra » Qua Jan 23, 2013 22:05
por brunadultra » Qua Jan 23, 2013 22:05
- 2 Respostas
- 6372 Exibições
- Última mensagem por Julliana_Ferrari

Qua Mar 02, 2016 01:32
Probabilidade
-
- QUESTÃO de Progressão Aritimética UNEB 2013
 por jessicaaangels » Sáb Set 28, 2013 11:59
por jessicaaangels » Sáb Set 28, 2013 11:59
- 2 Respostas
- 5095 Exibições
- Última mensagem por Thiago 86

Sex Out 11, 2013 12:27
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


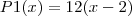

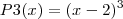

 P(x)=[(x-2)^2-12+6(x-2)](x-2)](/latexrender/pictures/8233fd5fe67f1372648e8f0e89880798.png)







