Olá , boa noite , gostaria que me ajudassem com esse problema :
- Preciso dividir - > 15x³-6x²-35x+14 por 3x²-7
Obrigada !



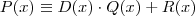
 e
e 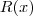 . Note que se
. Note que se 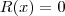 , então
, então 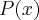 é divisível por
é divisível por 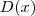 e
e  . Como resolver: procure montar um sistema como você aprendeu a fazer divisão de números, só que agora serão polinômios.
. Como resolver: procure montar um sistema como você aprendeu a fazer divisão de números, só que agora serão polinômios. 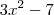 na chave e
na chave e  fora. Agora vamos ver: um fator
fora. Agora vamos ver: um fator  tal que
tal que 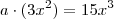 . Dividindo por
. Dividindo por  , com
, com  , encontramos que
, encontramos que 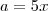 . Só que, ao fazer isso, também multiplicamos
. Só que, ao fazer isso, também multiplicamos 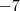 por
por 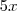 . Isso significa que, do polinômio inicial, subtraímos
. Isso significa que, do polinômio inicial, subtraímos 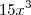 e
e  :
: 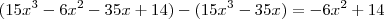 . Sobrou o polinômio
. Sobrou o polinômio 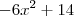 .
.  tal que
tal que 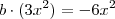 , e esse fator é
, e esse fator é  . Multiplicando por
. Multiplicando por 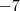 e subtraindo o polinômio resultante:
e subtraindo o polinômio resultante:  . Como o grau do divisor é maior que o grau do resto, a divisão pára e o resto
. Como o grau do divisor é maior que o grau do resto, a divisão pára e o resto 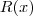 é o que sobrou. Veja:
é o que sobrou. Veja: 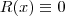 , portanto o polinômio
, portanto o polinômio  é divisível por
é divisível por 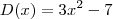 e
e 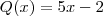 . Escrevendo na forma do algoritmo da divisão:
. Escrevendo na forma do algoritmo da divisão: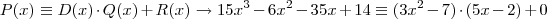



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.