 por adauto martins » Ter Nov 05, 2019 22:05
por adauto martins » Ter Nov 05, 2019 22:05
(ITA-instituto tecnologico de aeronautica-exame vestibular ?)
em que intervalo estao as raizes da equaçao
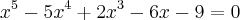
?
a)[-150,200] b)[-14,-12] c)[12,13] d)[-10,10] e)n.d.r
Editado pela última vez por
adauto martins em Ter Nov 05, 2019 22:38, em um total de 1 vez.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Nov 05, 2019 22:37
por adauto martins » Ter Nov 05, 2019 22:37
soluçao:
vamos fazer a cota inferior,ou seja:
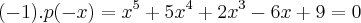
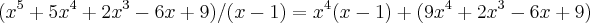
...
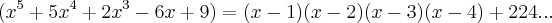
logo a cota inferior sera de -4,ou seja
![[-4,{c}_{s}] [-4,{c}_{s}]](/latexrender/pictures/ed0ca8cdb394eb9b31018757f3d9b1c8.png)
...deixo o calculo da cota-superior,que pelo proprio polinomio e metodo de "laguerre" e menor que 10...das alternativas apresentadas,podemos "afirmar ser a letra d)...
podemos ainda usar:
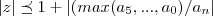
onde
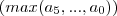
é o maior dos coefiecentes em em valor positivo de p(x)...em nosso caso
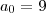
logo
![\left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]... \left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]...](/latexrender/pictures/f335078d5516bcefd94e7e06d906600e.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
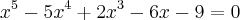 ?
?
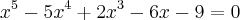 ?
?
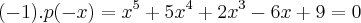
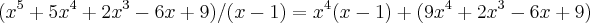
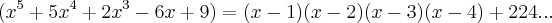
![[-4,{c}_{s}] [-4,{c}_{s}]](/latexrender/pictures/ed0ca8cdb394eb9b31018757f3d9b1c8.png) ...deixo o calculo da cota-superior,que pelo proprio polinomio e metodo de "laguerre" e menor que 10...das alternativas apresentadas,podemos "afirmar ser a letra d)...
...deixo o calculo da cota-superior,que pelo proprio polinomio e metodo de "laguerre" e menor que 10...das alternativas apresentadas,podemos "afirmar ser a letra d)...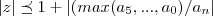
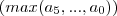
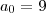
![\left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]... \left|z \right|\preceq 1+\left|9/1 \right|=1+9=10\Rightarrow
\left|z \right|\preceq 10\Rightarrow -10\preceq z \preceq 10
[-10,10]...](/latexrender/pictures/f335078d5516bcefd94e7e06d906600e.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

