Questão 14 (UNEB-2013) Ao desmontar um cubo de Rubik (cubo mágico), uma criança percebeu que ele era formado por
vinte e sete cubinhos menores e que dentre esses existiam oito cubinhos com três faces pintadas,
doze com apenas duas faces pintadas, seis com apenas uma das faces pintadas e apenas um
cubinho não possuía nenhuma das faces pintadas.
A tabela a seguir, mostra o número de cubinhos, de cada tipo, que podem ser obtidos ao dividir
a aresta de um cubo de madeira pintado, em partes iguais.
(tabela da questão segue em anexo)
Nessas condições, pode-se afirmar que, em R, a soma dos inversos das raízes do polinômio
P(x) = P3(x) ? P1(x) + P2(x) é igual a:
Resposta: 3/5


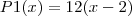

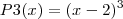

 P(x)=[(x-2)^2-12+6(x-2)](x-2)](/latexrender/pictures/8233fd5fe67f1372648e8f0e89880798.png)


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)