 por gutoponto7 » Qua Ago 15, 2012 10:30
por gutoponto7 » Qua Ago 15, 2012 10:30
Bom dia pessoal,
Primeiramente peço desculpas se criei o tópico no fórum errado, é meu primeiro tópico.
Enfim,
usando a forma de Lagrande, estou tentando encontrar o p2(x).
fiz a matrix e tudo, porém cheguei a esse resultado e NÃO estou conseguindo simplificar isso aí.
p2(x)=
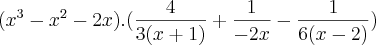
meu prof. passou que o resultado final simplificado será

Alguém poderia me dar umas dicas de como fazer? ou indicar algum artigo que eu possa ler pra entender como é feita essa operação?
Agradeço desde já

-
gutoponto7
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 13, 2012 11:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA CIVIL
- Andamento: cursando
 por e8group » Qua Ago 15, 2012 12:21
por e8group » Qua Ago 15, 2012 12:21
Perceba que ,

. Agora seja ,
x+1 = q
x-2 = p .
Assim segue que ,
![xqp\left[\frac{4}{6/2 p} - \frac{1}{6/3 x} -\frac{1}{6/2 q} }\right] xqp\left[\frac{4}{6/2 p} - \frac{1}{6/3 x} -\frac{1}{6/2 q} }\right]](/latexrender/pictures/17905a831076b7f60a61f838cedd1333.png)
![\frac{1}{6}[x(8q -p) -3pq ] . \frac{1}{6}[x(8q -p) -3pq ] .](/latexrender/pictures/4dd112b669e48bf013c3427ff0abeeee.png)
Substituindo fica ,
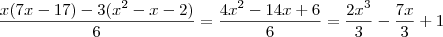
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Maneira mais eficiente para multiplicacao de fracoes algeb.
por lucas7 » Dom Fev 20, 2011 07:54
- 7 Respostas
- 3891 Exibições
- Última mensagem por lucas7

Seg Fev 21, 2011 16:38
Álgebra Elementar
-
- [Determinante] Dúvida multiplicação
por Perestroika » Dom Mar 16, 2014 17:09
- 3 Respostas
- 4994 Exibições
- Última mensagem por Cleyson007

Dom Mar 16, 2014 18:29
Matrizes e Determinantes
-
- Dúvida frações
por Andrewo » Qui Fev 16, 2012 09:28
- 1 Respostas
- 1052 Exibições
- Última mensagem por DanielFerreira

Ter Fev 21, 2012 16:30
Funções
-
- Dúvida em frações algébricas
por LuizCarlos » Dom Abr 22, 2012 10:04
- 7 Respostas
- 3229 Exibições
- Última mensagem por DanielFerreira

Qui Abr 26, 2012 20:14
Álgebra Elementar
-
- FRAÇÕES COM ARRANJOS - DÚVIDA EM EXERCÍCIO
por amateurfeet » Dom Mar 11, 2012 16:20
- 1 Respostas
- 2204 Exibições
- Última mensagem por LuizAquino

Seg Mar 12, 2012 12:57
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
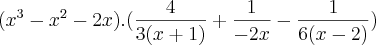




 . Agora seja ,
. Agora seja ,![xqp\left[\frac{4}{6/2 p} - \frac{1}{6/3 x} -\frac{1}{6/2 q} }\right] xqp\left[\frac{4}{6/2 p} - \frac{1}{6/3 x} -\frac{1}{6/2 q} }\right]](/latexrender/pictures/17905a831076b7f60a61f838cedd1333.png)
![\frac{1}{6}[x(8q -p) -3pq ] . \frac{1}{6}[x(8q -p) -3pq ] .](/latexrender/pictures/4dd112b669e48bf013c3427ff0abeeee.png) Substituindo fica ,
Substituindo fica ,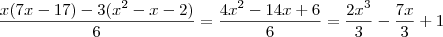 .
.