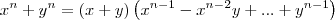
Bom, eu tenho '' a prova'' em um livro, só que eu não entendi a resolução. O exercício é parecido com um outro que postei aqui.
''De fato, como n é ímpar podemos escrever
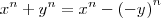 e aplicar a fórmula do item anterior, ou seja,
e aplicar a fórmula do item anterior, ou seja, 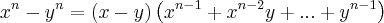 , colocando -y no lugar de y.
, colocando -y no lugar de y.Vejamos:
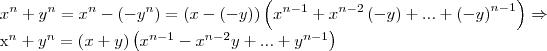
Bom, eu entendi que o cara substituiu y por - y entao x - (-y) tem de ficar positivo. Ok, mas nessa parte
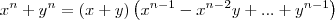 eu não entendo por que no final fica
eu não entendo por que no final fica 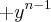 sendo que
sendo que 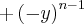 para mim é igual a
para mim é igual a 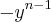 . Eu sei que se for par o número sempre será positivo. Mas quando for ímpar (que é o caso, não). Estou errado? Ou é o livro? Ou entendi errado? Grato desde já !
. Eu sei que se for par o número sempre será positivo. Mas quando for ímpar (que é o caso, não). Estou errado? Ou é o livro? Ou entendi errado? Grato desde já !

 é ímpar, então ele é da forma
é ímpar, então ele é da forma 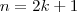 . Portanto,
. Portanto,  , mostrando que é par. Assim,
, mostrando que é par. Assim, 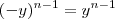 .
.



 .
.



