Exercício:
Sendo a , b e c as raizes da equação x³-2x²-6=0, calcule
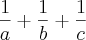 .
.Sugestão: reduza ao mesmo denominador a expressão
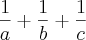 .
.O que eu tentei foi:
reduzir a um único denominador:
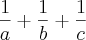 =
= 
p(x)= x³-2x²-6=0 e a , b e c são raizes então:
p(a)= a³-2a²-6=0
p(b)= b³-2b²-6=0
p(c)= c³-2c²-6=0
x=a
x-a=0
x=b
x-b=0
x=c
x-c=0
Espero que alguem entenda!



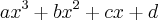
 I
I II
II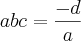 III
III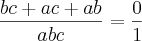






 .
.



