 por Andreza » Ter Nov 08, 2011 12:45
por Andreza » Ter Nov 08, 2011 12:45
O polinômio
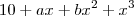
é divisível por (x-1) (x-2).
Neste caso quanto vale b-a?
Eu coloquei o polinômio em ordem decrescente de coeficientes e efetuei a divisão mas nao consegui encontrar o valor de a e b para efetuar a subtração.
Eu cheguei ao quociente x+4 e resto b+11ax. Como faço pra encontrar a e b?
Desde já agradeço.
Eu desconsiderei essa divisão feita acima e montei um sistema colocando as raízes do polinômio no lugar de x.
Eu encontrei a+b=11 e 2a+4b=-18. Resolvendo o sitema eu encontrei a=-13 e b=2.
Daí fazendo b-a= 2-(-13)= 2+13=15 Será q está certo ? Desde já agradeço!!!!
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por LuizAquino » Sáb Nov 12, 2011 08:53
por LuizAquino » Sáb Nov 12, 2011 08:53
Andreza escreveu:O polinômio
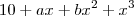
é divisível por
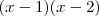
.
Neste caso quanto vale b-a?
Andreza escreveu:(...) montei um sistema colocando as raízes do polinômio no lugar de x.
Eu encontrei a+b=11 e 2a+4b=-18. Resolvendo o sitema eu encontrei a=-13 e b=2.
Você apenas esqueceu de escrever um sinal na primeira equação: a + b = -11.
A solução do sistema é de fato a = -13 e b = 2.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Andreza » Sáb Nov 12, 2011 09:49
por Andreza » Sáb Nov 12, 2011 09:49
É verdade; a+b=-11.
Muito obrigada.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Valor de Mercadoria] A partir do valor total de venda
por Gerson Belini » Qua Out 02, 2013 02:17
- 0 Respostas
- 3901 Exibições
- Última mensagem por Gerson Belini

Qua Out 02, 2013 02:17
Matemática Financeira
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3856 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:41
Trigonometria
-
- valor bruto a partir do valor liquido
por juan cunha » Ter Mai 03, 2016 10:29
- 3 Respostas
- 17790 Exibições
- Última mensagem por nakagumahissao

Sáb Mai 07, 2016 22:51
Matemática Financeira
-
- Valor de i que maximiza o valor do lucro
por filipeferminiano » Qui Jun 23, 2011 14:41
- 3 Respostas
- 4576 Exibições
- Última mensagem por LuizAquino

Sáb Ago 27, 2011 22:45
Cálculo
-
- valor da distribuição e valor da esperança
por Ana Maria da Silva » Sex Abr 11, 2014 00:12
- 1 Respostas
- 2468 Exibições
- Última mensagem por fff

Sex Abr 11, 2014 15:31
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
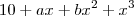 é divisível por (x-1) (x-2).
é divisível por (x-1) (x-2).

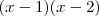 .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

