![\frac{1}{\sqrt[2]{k^2+1}-k} \frac{1}{\sqrt[2]{k^2+1}-k}](/latexrender/pictures/a6d43a5b2c94ca6fa25b61d669b04acd.png)
Alternativas:
A)Diminui quando k aumenta
B) é menor que 0
C) está entre 0 e k
D) Está entre k e 2k
E) é maior que 2k
Alguma luz?

![\frac{1}{\sqrt[2]{k^2+1}-k} \frac{1}{\sqrt[2]{k^2+1}-k}](/latexrender/pictures/a6d43a5b2c94ca6fa25b61d669b04acd.png)

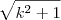 é quase igual a k, porém é maior (por um pequeno valor). Porém, quando k aumenta, o valor do denominador (parte inferior da fração) diminui. Exemplo:
é quase igual a k, porém é maior (por um pequeno valor). Porém, quando k aumenta, o valor do denominador (parte inferior da fração) diminui. Exemplo:




Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: