 por victorleme » Dom Mai 08, 2011 16:33
por victorleme » Dom Mai 08, 2011 16:33
1)Se k é um número real maior que zero, então :![\frac{1}{\sqrt[2]{k^2+1}-k} \frac{1}{\sqrt[2]{k^2+1}-k}](/latexrender/pictures/a6d43a5b2c94ca6fa25b61d669b04acd.png)
Alternativas:
A)Diminui quando k aumenta
B) é menor que 0
C) está entre 0 e k
D) Está entre k e 2k
E) é maior que 2kAlguma luz?
-
victorleme
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 23, 2011 19:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Mecatrônica
- Andamento: cursando
 por Molina » Dom Mai 08, 2011 17:08
por Molina » Dom Mai 08, 2011 17:08
Boa tarde, Victor.
Perceba que
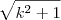
é
quase igual a k, porém
é maior (por um pequeno valor). Porém, quando k aumenta, o valor do denominador (parte inferior da fração) diminui. Exemplo:


Ou seja, a expressão completa
aumenta quando
k aumenta. (alternativa
A está descartada).
O denominador da fração é sempre um valor positivo pelo critério imposto no enunciado, logo a expressão total será sempre
positiva. (alternativa
B está descartada).
Para verificar as alternativas
[u]C[/u],
D e
E podemos pegar um k particular e ver o que vamos obter como resposta:

Concluimos que a alternativa
E está correta.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função ( Estudo do sinal )
por clara » Dom Jun 21, 2009 20:55
- 1 Respostas
- 5319 Exibições
- Última mensagem por Molina

Seg Jun 22, 2009 12:57
Funções
-
- Derivada estudo de sinal
por Carolminera » Dom Jul 06, 2014 15:02
- 1 Respostas
- 1751 Exibições
- Última mensagem por e8group

Dom Jul 06, 2014 20:35
Cálculo: Limites, Derivadas e Integrais
-
- Estudo da variação de sinal
por mayaracalixta » Qua Mar 02, 2016 23:50
- 0 Respostas
- 1261 Exibições
- Última mensagem por mayaracalixta

Qua Mar 02, 2016 23:50
Funções
-
- [Estudo de sinal dessa função]
por wilsonfilho0 » Ter Jun 14, 2016 17:06
- 1 Respostas
- 2456 Exibições
- Última mensagem por vitor_jo

Dom Jul 10, 2016 04:53
Funções
-
- [Funções] Estudo do sinal, domínio e gráficos
por Fernanda Almeida » Dom Ago 04, 2013 16:12
- 1 Respostas
- 1739 Exibições
- Última mensagem por nakagumahissao

Qua Out 07, 2015 14:30
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{1}{\sqrt[2]{k^2+1}-k} \frac{1}{\sqrt[2]{k^2+1}-k}](/latexrender/pictures/a6d43a5b2c94ca6fa25b61d669b04acd.png)

![\frac{1}{\sqrt[2]{k^2+1}-k} \frac{1}{\sqrt[2]{k^2+1}-k}](/latexrender/pictures/a6d43a5b2c94ca6fa25b61d669b04acd.png)

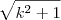 é quase igual a k, porém é maior (por um pequeno valor). Porém, quando k aumenta, o valor do denominador (parte inferior da fração) diminui. Exemplo:
é quase igual a k, porém é maior (por um pequeno valor). Porém, quando k aumenta, o valor do denominador (parte inferior da fração) diminui. Exemplo:




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.