 por Rose » Seg Set 08, 2008 22:07
por Rose » Seg Set 08, 2008 22:07
OLá!!
Não estou sabendo como fazer este problema sobre polinômios. Gostaria que vocês me ajudassem.
Questão: Determine o polinômio com coeficientes inteiros que tenha raiz de 3 + raiz 2 como uma de suas raizes.
Obrigada
-
Rose
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qui Mai 15, 2008 14:13
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Ter Set 09, 2008 21:33
por admin » Ter Set 09, 2008 21:33
Olá
Rose!
Pelo
teorema da decomposição, todo polinômio

de grau

(

)
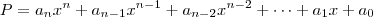
pode ser decomposto de maneira única em

fatores do primeiro grau.
Desta forma, podemos reescrevê-lo assim:

onde

são as raízes de

.
Sendo assim, se

é raiz, então:
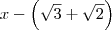
divide o polinômio.
Em outras palavras,

é múltiplo de
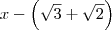
.
Como sabemos apenas esta raiz, uma alternativa é supor

e avaliarmos o produto:
![P' = \left[ x-\left( \sqrt{3}+\sqrt{2} \right) \right] \cdot \left[ x+\left( \sqrt{3}+\sqrt{2} \right) \right] P' = \left[ x-\left( \sqrt{3}+\sqrt{2} \right) \right] \cdot \left[ x+\left( \sqrt{3}+\sqrt{2} \right) \right]](/latexrender/pictures/ef23a12ce403dc05f3383c65372c30ff.png)
sendo o outro fator o conjugado, pois estamos em busca de coeficientes inteiros.
Faça a distributiva e caso não obtenha coeficientes inteiros, multiplique novamente por um fator "conjugado" ao polinômio atual, visando eliminar as raízes dos coeficientes.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Rose » Qua Set 10, 2008 11:50
por Rose » Qua Set 10, 2008 11:50
OLá!!
Obrigadaaa!!!
Depois desta explicação, consegui entender o teorema da decomposição e sua utilidade. Resolvi e cheguei a um polinômio de grau 4. Valeu genteee!!!!
-
Rose
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Qui Mai 15, 2008 14:13
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Polinômios] Grau do Polinômios e +
por Warioboy » Ter Mai 29, 2012 15:06
- 5 Respostas
- 8356 Exibições
- Última mensagem por Cleyson007

Dom Jun 03, 2012 16:18
Polinômios
-
- Polinômios - 3
por DanielFerreira » Ter Set 22, 2009 13:59
- 3 Respostas
- 3077 Exibições
- Última mensagem por DanielFerreira

Qui Fev 10, 2011 09:26
Polinômios
-
- Polinômios - 2
por DanielFerreira » Ter Set 22, 2009 14:00
- 1 Respostas
- 3247 Exibições
- Última mensagem por thadeu

Seg Nov 02, 2009 11:47
Polinômios
-
- Polinômios
por DanielFerreira » Ter Set 22, 2009 14:01
- 2 Respostas
- 2448 Exibições
- Última mensagem por DanielFerreira

Qui Nov 19, 2009 17:59
Polinômios
-
- Polinômios - 4
por DanielFerreira » Ter Set 22, 2009 14:04
- 4 Respostas
- 4009 Exibições
- Última mensagem por DanielFerreira

Qua Fev 09, 2011 13:39
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 de grau
de grau  (
( )
)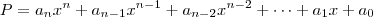
 fatores do primeiro grau.
fatores do primeiro grau.
 são as raízes de
são as raízes de  .
. é raiz, então:
é raiz, então: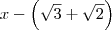 divide o polinômio.
divide o polinômio. é múltiplo de
é múltiplo de 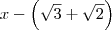 .
. e avaliarmos o produto:
e avaliarmos o produto:![P' = \left[ x-\left( \sqrt{3}+\sqrt{2} \right) \right] \cdot \left[ x+\left( \sqrt{3}+\sqrt{2} \right) \right] P' = \left[ x-\left( \sqrt{3}+\sqrt{2} \right) \right] \cdot \left[ x+\left( \sqrt{3}+\sqrt{2} \right) \right]](/latexrender/pictures/ef23a12ce403dc05f3383c65372c30ff.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
