ela é assim
Considere o número complexo .
 .
.(a) Prove que
 .
.(b) Prove que
 .
.e como Dica eu tenho:
 .
.
 .
. .
. .
. .
.
muxapore escreveu:
Considere o número complexo ..
 . Onde
. Onde  é chamado de parte real do número complexo e
é chamado de parte real do número complexo e  é chamado de parte imaginária do numero complexo. No seu caso temos
é chamado de parte imaginária do numero complexo. No seu caso temos  . Qual é o
. Qual é o  e qual é o
e qual é o  nesse número?
nesse número?(a) Prove que.
 . É só você substituir e fazer as contas.
. É só você substituir e fazer as contas.(b) Prove que.
e como Dica eu tenho:.
 (
(  e
e 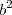 você já calculou no item a, lembrar também que
você já calculou no item a, lembrar também que 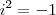 ). Basta então substituir, usar a dica e fazer as contas. Salvo algum probleminha de sinal, você deverá chegar ao resultado.
). Basta então substituir, usar a dica e fazer as contas. Salvo algum probleminha de sinal, você deverá chegar ao resultado.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
