 por adauto martins » Ter Out 15, 2019 23:41
por adauto martins » Ter Out 15, 2019 23:41
(IME-instituto militar de engenharia-exame 1959)
um numero complexo variavel tem,para a parte real, os valores
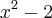
e para parte imaginaria
![x\sqrt[]{2} x\sqrt[]{2}](/latexrender/pictures/72ae2b5c4db703ef121fb4972aa73f34.png)
.qual o valor minimo do modulo desse numero?
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Out 15, 2019 23:54
por adauto martins » Ter Out 15, 2019 23:54
soluçao:
o numero em questao é:
![z=({x}^{2}-2)+(x\sqrt[]{2})i z=({x}^{2}-2)+(x\sqrt[]{2})i](/latexrender/pictures/615d8bb58a5fb426a800d28e83bf3e04.png)
cujo modulo é calculado,como se segue:
![\left|z \right|=\sqrt[]{{({x}^{2}-2)}^{2}+({x\sqrt[]{2}}^{2})}... \left|z \right|=\sqrt[]{{({x}^{2}-2)}^{2}+({x\sqrt[]{2}}^{2})}...](/latexrender/pictures/d9d5cee7c6bd1b607eca8c36c370cdf3.png)
o que fazendo as contas e os algebrimos simples,chegaremos em:
![\left|z \right|=\sqrt[]{{x}^{4}-2{x}^{2}-1} \left|z \right|=\sqrt[]{{x}^{4}-2{x}^{2}-1}](/latexrender/pictures/cbc3a2b48c4c3f017cae9b708c9dcccb.png)
derivando e igualdado a zero,teremos:
![d/x(\left|z \right|)=(-1/2)(\sqrt[]{(4{x}^{3}-4x})/({x}^{4}-2x+4)=0
\Rightarrow 4x(x-1)\Rightarrow x=1 d/x(\left|z \right|)=(-1/2)(\sqrt[]{(4{x}^{3}-4x})/({x}^{4}-2x+4)=0
\Rightarrow 4x(x-1)\Rightarrow x=1](/latexrender/pictures/22cb2ec9e0308bbca36100b0abbdfa36.png)
substituindo em
![(\left|z \right|)=\sqrt[]{1-2+4}=\sqrt[]{3} (\left|z \right|)=\sqrt[]{1-2+4}=\sqrt[]{3}](/latexrender/pictures/fe4dfeef1179c7d4f1b20e8a4b028c96.png)
para confirmar o minimo teriamos q. calcular a derivada segunda e ver q. ela assuime o valor negativo,isso deixo para os interessados...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qua Out 16, 2019 17:24
por adauto martins » Qua Out 16, 2019 17:24
uma correçao,alias duas,mas o resultado é o calculado.
![(d/dx)\left|z \right|=(1/2).(4.{x}^{3}-4x)/(\sqrt[]{({x}^{4}-2x1)} (d/dx)\left|z \right|=(1/2).(4.{x}^{3}-4x)/(\sqrt[]{({x}^{4}-2x1)}](/latexrender/pictures/5b5a4b93915b78aee4153f7728aa8385.png)
e no caso de ponto de minimo a derivada seg. de

é negativa(ponto de minimo)
...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
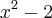 e para parte imaginaria
e para parte imaginaria ![x\sqrt[]{2} x\sqrt[]{2}](/latexrender/pictures/72ae2b5c4db703ef121fb4972aa73f34.png) .qual o valor minimo do modulo desse numero?
.qual o valor minimo do modulo desse numero?
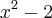 e para parte imaginaria
e para parte imaginaria ![x\sqrt[]{2} x\sqrt[]{2}](/latexrender/pictures/72ae2b5c4db703ef121fb4972aa73f34.png) .qual o valor minimo do modulo desse numero?
.qual o valor minimo do modulo desse numero?
![z=({x}^{2}-2)+(x\sqrt[]{2})i z=({x}^{2}-2)+(x\sqrt[]{2})i](/latexrender/pictures/615d8bb58a5fb426a800d28e83bf3e04.png)
![\left|z \right|=\sqrt[]{{({x}^{2}-2)}^{2}+({x\sqrt[]{2}}^{2})}... \left|z \right|=\sqrt[]{{({x}^{2}-2)}^{2}+({x\sqrt[]{2}}^{2})}...](/latexrender/pictures/d9d5cee7c6bd1b607eca8c36c370cdf3.png)
![\left|z \right|=\sqrt[]{{x}^{4}-2{x}^{2}-1} \left|z \right|=\sqrt[]{{x}^{4}-2{x}^{2}-1}](/latexrender/pictures/cbc3a2b48c4c3f017cae9b708c9dcccb.png)
![d/x(\left|z \right|)=(-1/2)(\sqrt[]{(4{x}^{3}-4x})/({x}^{4}-2x+4)=0
\Rightarrow 4x(x-1)\Rightarrow x=1 d/x(\left|z \right|)=(-1/2)(\sqrt[]{(4{x}^{3}-4x})/({x}^{4}-2x+4)=0
\Rightarrow 4x(x-1)\Rightarrow x=1](/latexrender/pictures/22cb2ec9e0308bbca36100b0abbdfa36.png)
![(\left|z \right|)=\sqrt[]{1-2+4}=\sqrt[]{3} (\left|z \right|)=\sqrt[]{1-2+4}=\sqrt[]{3}](/latexrender/pictures/fe4dfeef1179c7d4f1b20e8a4b028c96.png)

![(d/dx)\left|z \right|=(1/2).(4.{x}^{3}-4x)/(\sqrt[]{({x}^{4}-2x1)} (d/dx)\left|z \right|=(1/2).(4.{x}^{3}-4x)/(\sqrt[]{({x}^{4}-2x1)}](/latexrender/pictures/5b5a4b93915b78aee4153f7728aa8385.png)
 é negativa(ponto de minimo)
é negativa(ponto de minimo)