 por futuromilitar » Qui Mai 26, 2016 22:08
por futuromilitar » Qui Mai 26, 2016 22:08
Sendo

divisível por

, a média geometrica das raízes complexas é:
a)1
b)
![\sqrt[2]{i} \sqrt[2]{i}](/latexrender/pictures/1aef6795ad8fc4ae2aaf358178bcd48a.png)
c)
![-\sqrt[2]{i} -\sqrt[2]{i}](/latexrender/pictures/c65f6492f76e1c0b2e34229964b03b4e.png)
d)i
"Nenhum soldado pode combater a não ser que esteja bem abastecido de carne e cerveja''
-

futuromilitar
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 19, 2016 17:50
- Localização: Itapajé,Ceará,Brasil
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Contabilidade
- Andamento: formado
 por DanielFerreira » Ter Mai 31, 2016 00:44
por DanielFerreira » Ter Mai 31, 2016 00:44
Ora, se
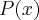
é divisível por

, então

.
Com isso,
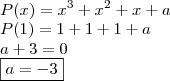
Efectuando a divisão,
+ x³ + x² + x - 3 |
x - 1--------------------| x² + 2x + 3
+ x³ + x²
- x³ + x²
---------------------
+ 2x² + x - 3
- 2x² + 2x
---------------------
+ 3x - 3
- 3x + 3
---------------------
0
Resolvendo a equação

:
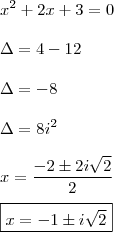
Por fim, calculamos a média geométrica entre
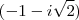
e
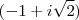
. Daí,
![\\ M_g = \sqrt[2]{(- 1 - i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(1 + i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(- 1 + i^2 \cdot 2)} \\\\ M_g = \sqrt[2]{- (- 1 - 2)} \\\\ \boxed{\boxed{M_g = \sqrt{3}}} \\ M_g = \sqrt[2]{(- 1 - i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(1 + i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(- 1 + i^2 \cdot 2)} \\\\ M_g = \sqrt[2]{- (- 1 - 2)} \\\\ \boxed{\boxed{M_g = \sqrt{3}}}](/latexrender/pictures/9fcbc91d92461faefe7702822409e324.png)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 divisível por
divisível por  , a média geometrica das raízes complexas é:
, a média geometrica das raízes complexas é:![\sqrt[2]{i} \sqrt[2]{i}](/latexrender/pictures/1aef6795ad8fc4ae2aaf358178bcd48a.png)
![-\sqrt[2]{i} -\sqrt[2]{i}](/latexrender/pictures/c65f6492f76e1c0b2e34229964b03b4e.png)

 divisível por
divisível por  , a média geometrica das raízes complexas é:
, a média geometrica das raízes complexas é:![\sqrt[2]{i} \sqrt[2]{i}](/latexrender/pictures/1aef6795ad8fc4ae2aaf358178bcd48a.png)
![-\sqrt[2]{i} -\sqrt[2]{i}](/latexrender/pictures/c65f6492f76e1c0b2e34229964b03b4e.png)

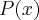 é divisível por
é divisível por  , então
, então  .
.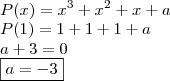
 :
: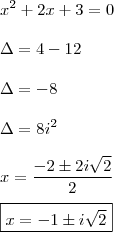
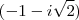 e
e 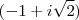 . Daí,
. Daí,![\\ M_g = \sqrt[2]{(- 1 - i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(1 + i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(- 1 + i^2 \cdot 2)} \\\\ M_g = \sqrt[2]{- (- 1 - 2)} \\\\ \boxed{\boxed{M_g = \sqrt{3}}} \\ M_g = \sqrt[2]{(- 1 - i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(1 + i\sqrt{2})(- 1 + i\sqrt{2})} \\\\ M_g = \sqrt[2]{-(- 1 + i^2 \cdot 2)} \\\\ M_g = \sqrt[2]{- (- 1 - 2)} \\\\ \boxed{\boxed{M_g = \sqrt{3}}}](/latexrender/pictures/9fcbc91d92461faefe7702822409e324.png)

