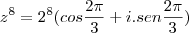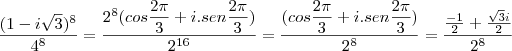por geriane » Seg Jul 05, 2010 12:16
por geriane » Seg Jul 05, 2010 12:16
Calcule o módulo do complexo
![{(\frac{4}{1-i\sqrt[2]{3}}})^{-8} {(\frac{4}{1-i\sqrt[2]{3}}})^{-8}](/latexrender/pictures/36f0403a8ced816b1e2a4b21064a9a54.png)
.
Obrigada!
-
geriane
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Sáb Abr 03, 2010 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: formado
 por Tom » Seg Jul 05, 2010 12:57
por Tom » Seg Jul 05, 2010 12:57
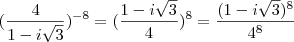
Analisemos :

:
Usando as definições:

e o argumento de

é
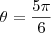
Assim, escrevendo

na forma polar:
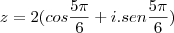
e usando a propriedade de potenciação para complexos:

e , com a redução do arco ao primeiro quadrente,
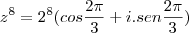
Voltando a expressão:
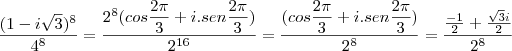
Finalmente, o valor da expressão é:

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por geriane » Seg Jul 05, 2010 13:34
por geriane » Seg Jul 05, 2010 13:34
Tom, fico muito agradecida só que o resultado final do exercício é 1/256 e não estou conseguindo chegar a esse resultado eu fiz dessa maneira que você fez só q não consigo chegar ao resultado.
-
geriane
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Sáb Abr 03, 2010 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: formado
 por Elcioschin » Seg Jul 05, 2010 16:10
por Elcioschin » Seg Jul 05, 2010 16:10
Tom/Geriane
A solução do Tom, esta perfeita do ponto de vista do encaminhamento. Faltou apenas:
a) Corrigir um pequeno erro de cálculo do argumento
b) Calcular o módulo no final
z = 1 - i*V3 ----> z = 2*(1/2 - i*V3/2) ----> ângulo do 4º quadrante ---> z = 2*[cos(5pi/3) + isen(5pi/3)]
Assim ----> teta = 5pi/3
z^8 = (2^8)*[cos(8*5pi/3) + i*sen(8*5pi/3)] ----> z = 2*[cos(40*pi/3) + i*sen(40*pi/3)]
Reduzindo ao 1º quadrante ---> z = (2~8)*[cos(4pi/3) +i*sen(4pi/3)]
z = (2^8)*[- 1/2 - i*V3/2)
Neste caso o valor da expressão é (- 1 - V3*i)/512
|z|² = (1/512)²*[(-1)² + (-V3)²] ---> |z|² = (1/512)²*(1 + 3) ----> |z|² = 4/512² ----> |z|² = 2²/512²
|z = 2/512 ----> |z| = 1/256
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por geriane » Seg Jul 05, 2010 17:00
por geriane » Seg Jul 05, 2010 17:00
Obrigada Tom e Elcio pela atenção !!!!!!!!!
-
geriane
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Sáb Abr 03, 2010 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: formado
 por Tom » Seg Jul 05, 2010 23:04
por Tom » Seg Jul 05, 2010 23:04
Desculpe, acho que copiei errado quando passei a questão pro caderno.

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números Complexos na forma trigonométrica 2
por geriane » Seg Jul 05, 2010 14:11
- 1 Respostas
- 3224 Exibições
- Última mensagem por Elcioschin

Seg Jul 05, 2010 15:23
Números Complexos
-
- Números Complexos na forma trigonométrica 3
por geriane » Seg Jul 05, 2010 14:16
- 1 Respostas
- 2110 Exibições
- Última mensagem por Elcioschin

Seg Jul 05, 2010 15:18
Números Complexos
-
- Multiplicação de números complexos na forma polar
por Torres » Sex Jun 14, 2013 00:51
- 4 Respostas
- 3841 Exibições
- Última mensagem por Torres

Sáb Jun 15, 2013 15:56
Números Complexos
-
- [Numeros Complexos] Forma polar e cartesiana de w1 e w2
por karenfreitas » Dom Dez 04, 2016 16:36
- 0 Respostas
- 5247 Exibições
- Última mensagem por karenfreitas

Dom Dez 04, 2016 16:36
Números Complexos
-
- passe para a forma algebrica os numeros complexos
por mary leal » Qui Nov 19, 2009 01:10
- 2 Respostas
- 4387 Exibições
- Última mensagem por mary leal

Sex Nov 20, 2009 02:59
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{(\frac{4}{1-i\sqrt[2]{3}}})^{-8} {(\frac{4}{1-i\sqrt[2]{3}}})^{-8}](/latexrender/pictures/36f0403a8ced816b1e2a4b21064a9a54.png) .
.
![{(\frac{4}{1-i\sqrt[2]{3}}})^{-8} {(\frac{4}{1-i\sqrt[2]{3}}})^{-8}](/latexrender/pictures/36f0403a8ced816b1e2a4b21064a9a54.png) .
.
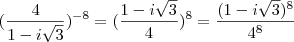
 :
: e o argumento de
e o argumento de  é
é 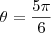
 na forma polar:
na forma polar: 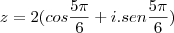 e usando a propriedade de potenciação para complexos:
e usando a propriedade de potenciação para complexos: e , com a redução do arco ao primeiro quadrente,
e , com a redução do arco ao primeiro quadrente,