 por JKS » Qui Jun 20, 2013 01:32
por JKS » Qui Jun 20, 2013 01:32
Não consigo.. se alguém puder me ajudar ..
Determine dois números complexos z1 e z2 tais que
![\left[z1 \right]=\left|z2 \right|=1 \left[z1 \right]=\left|z2 \right|=1](/latexrender/pictures/fb7549dc4c9f9277e7342078dc7b5f34.png)
e z1+z2=1.
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Dom Jul 21, 2013 22:35
por fraol » Dom Jul 21, 2013 22:35
Boa noite,
Vamos considerar os dois números complexos:

e

De
![\left|z_1 \right| = 1 \Rightarrow x_1^2 + y_1^2 = 1 \Leftrightarrow y_1 = \sqrt[2]{1-x_1^2} \left|z_1 \right| = 1 \Rightarrow x_1^2 + y_1^2 = 1 \Leftrightarrow y_1 = \sqrt[2]{1-x_1^2}](/latexrender/pictures/6858e71ba4a5c4b246213f90e1673350.png)
.
De

e
![y_1 + y_2 = 0 \Leftrightarrow y_2 = - y_1 = - \sqrt[2]{1-x_1^2} y_1 + y_2 = 0 \Leftrightarrow y_2 = - y_1 = - \sqrt[2]{1-x_1^2}](/latexrender/pictures/a7bf6e8eb39c096f9bd3359b0d158485.png)
.
De
![\left|z_2 \right| = 1 \Rightarrow x_2^2 + y_2^2 = 1 \Leftrightarrow (1-x_1)^2 + \left(- \sqrt[2]{1-x_1^2} \right)^2 = 1 \left|z_2 \right| = 1 \Rightarrow x_2^2 + y_2^2 = 1 \Leftrightarrow (1-x_1)^2 + \left(- \sqrt[2]{1-x_1^2} \right)^2 = 1](/latexrender/pictures/1801c69aa639ff158640f8d8fc5d378d.png)
então
![x_1 = \frac{1}{2}, y_1 = \sqrt[2]{\frac{3}{4}}, x_2 = \frac{1}{2}, y_1 = - \sqrt[2]{\frac{3}{4}} x_1 = \frac{1}{2}, y_1 = \sqrt[2]{\frac{3}{4}}, x_2 = \frac{1}{2}, y_1 = - \sqrt[2]{\frac{3}{4}}](/latexrender/pictures/0a45325ef9cd1c2ebb42463269876f8c.png)
.
Agora basta substituir esses valores nas expressões de

e
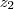
para completar.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Números complexos] Determinar a^b
por belguilhem » Sáb Ago 20, 2011 17:50
- 3 Respostas
- 2210 Exibições
- Última mensagem por belguilhem

Sáb Ago 20, 2011 21:13
Números Complexos
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17106 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Determinar 5 números de uma PG
por Carolziiinhaaah » Qua Jun 16, 2010 14:11
- 2 Respostas
- 1369 Exibições
- Última mensagem por Carolziiinhaaah

Qua Jun 16, 2010 15:11
Progressões
-
- Determinar os numeros criticos
por Vencill » Qua Dez 03, 2014 17:42
- 3 Respostas
- 1893 Exibições
- Última mensagem por Cleyson007

Qui Dez 04, 2014 08:21
Funções
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13317 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left[z1 \right]=\left|z2 \right|=1 \left[z1 \right]=\left|z2 \right|=1](/latexrender/pictures/fb7549dc4c9f9277e7342078dc7b5f34.png) e z1+z2=1.
e z1+z2=1.
![\left[z1 \right]=\left|z2 \right|=1 \left[z1 \right]=\left|z2 \right|=1](/latexrender/pictures/fb7549dc4c9f9277e7342078dc7b5f34.png) e z1+z2=1.
e z1+z2=1.
 e
e 
![\left|z_1 \right| = 1 \Rightarrow x_1^2 + y_1^2 = 1 \Leftrightarrow y_1 = \sqrt[2]{1-x_1^2} \left|z_1 \right| = 1 \Rightarrow x_1^2 + y_1^2 = 1 \Leftrightarrow y_1 = \sqrt[2]{1-x_1^2}](/latexrender/pictures/6858e71ba4a5c4b246213f90e1673350.png) .
. e
e ![y_1 + y_2 = 0 \Leftrightarrow y_2 = - y_1 = - \sqrt[2]{1-x_1^2} y_1 + y_2 = 0 \Leftrightarrow y_2 = - y_1 = - \sqrt[2]{1-x_1^2}](/latexrender/pictures/a7bf6e8eb39c096f9bd3359b0d158485.png) .
.![\left|z_2 \right| = 1 \Rightarrow x_2^2 + y_2^2 = 1 \Leftrightarrow (1-x_1)^2 + \left(- \sqrt[2]{1-x_1^2} \right)^2 = 1 \left|z_2 \right| = 1 \Rightarrow x_2^2 + y_2^2 = 1 \Leftrightarrow (1-x_1)^2 + \left(- \sqrt[2]{1-x_1^2} \right)^2 = 1](/latexrender/pictures/1801c69aa639ff158640f8d8fc5d378d.png) então
então ![x_1 = \frac{1}{2}, y_1 = \sqrt[2]{\frac{3}{4}}, x_2 = \frac{1}{2}, y_1 = - \sqrt[2]{\frac{3}{4}} x_1 = \frac{1}{2}, y_1 = \sqrt[2]{\frac{3}{4}}, x_2 = \frac{1}{2}, y_1 = - \sqrt[2]{\frac{3}{4}}](/latexrender/pictures/0a45325ef9cd1c2ebb42463269876f8c.png) .
. e
e 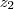 para completar.
para completar.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.