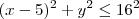por Andreza » Sáb Out 22, 2011 11:23
por Andreza » Sáb Out 22, 2011 11:23
36) O conjunto dos pontos do plano que verificam a condição |z – 5 | ? 16 é:
Eu resolvi a inequação normal e cheguei a solução um segmento de comprimento igual a 21( mas na verdade é menor ou igual, opção q nao tinha na prova ). Errei a questão pq a resposta correta é um disco de raio 16. Já pesquisei e estudei os números complexos mas não consegui resolvê-la ainda. Desde já agradeço. Aguardo resposta.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por MarceloFantini » Sáb Out 22, 2011 15:21
por MarceloFantini » Sáb Out 22, 2011 15:21
Sendo
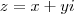
, teremos
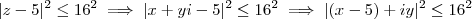
. Daí, podemos concluir:
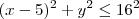
Que é a equação de um disco de raio 16 e centro em (5,0).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [módulo número complexo] Ajuda questao
por filipetrr » Qui Jun 27, 2013 10:43
- 5 Respostas
- 7289 Exibições
- Última mensagem por adauto martins

Qui Jan 08, 2015 11:28
Números Complexos
-
- [módulo do número complexo]
por JKS » Qui Jun 20, 2013 01:56
- 1 Respostas
- 3051 Exibições
- Última mensagem por MateusL

Qui Jul 18, 2013 19:49
Números Complexos
-
- Módulo de um número complexo, ajuda por favor!
por elisamaria » Qua Mai 13, 2015 15:19
- 0 Respostas
- 3468 Exibições
- Última mensagem por elisamaria

Qua Mai 13, 2015 15:19
Números Complexos
-
- Questão de Concurso-Número Complexos
por Pri Ferreira » Qua Mar 21, 2012 13:44
- 1 Respostas
- 1580 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 15:31
Números Complexos
-
- Equação de número complexo
 por YuriFreire » Seg Set 01, 2014 21:44
por YuriFreire » Seg Set 01, 2014 21:44
- 3 Respostas
- 5126 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 21:19
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


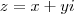 , teremos
, teremos 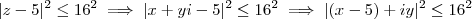 . Daí, podemos concluir:
. Daí, podemos concluir: