 por Anniinha » Dom Out 31, 2010 02:32
por Anniinha » Dom Out 31, 2010 02:32
como se resolve essa questão:
z² - (8 - 5i)z + 40 - 20i = 0??
o que eu ja fiz:
![z = - (8-5i) \frac{+}{} [\right]\sqrt[]{(8 - 5i)^{2} - (4).(1).(-20)}\left] / 2 z = - (8-5i) \frac{+}{} [\right]\sqrt[]{(8 - 5i)^{2} - (4).(1).(-20)}\left] / 2](/latexrender/pictures/b0f1b1348627677628aa3c7c567a658e.png)
colocando o 2 para dentro da raíz:
![z= \frac{-8 + 5i}{2} \frac{+}{} \sqrt[]{\frac{89}{4}+ 20i} z= \frac{-8 + 5i}{2} \frac{+}{} \sqrt[]{\frac{89}{4}+ 20i}](/latexrender/pictures/f0f99bacf59763c64689d40d3d13b5c8.png)
depois tentei resolver a raiz.
![{\left( \sqrt[]{\frac{89}{4}+ 20i} \right)}^{\frac{1}{2}} {\left( \sqrt[]{\frac{89}{4}+ 20i} \right)}^{\frac{1}{2}}](/latexrender/pictures/e3dcc87e1ad33de9e15a06f745c4c6fb.png)
onde tenho que
![z = \frac{89}{4}+ 20i ; n=2 ; \left|r \right| = 895 >>\left|r \right|= \sqrt[]{{x}^{2} + {y}^{2}} z = \frac{89}{4}+ 20i ; n=2 ; \left|r \right| = 895 >>\left|r \right|= \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/fb5a9b39ab9a932499cfbfacd8d8deb2.png)
depois disso nao sei fazer, estou me complicando também na hora de calcular o teta, que eu sei que é a
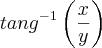
, soh lembrando que z = x + iy
entao, alguém pode me ajudar?? ^^
-

Anniinha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Out 31, 2010 01:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geofísica
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equação do 2ºgrau
por jose henrique » Seg Set 13, 2010 09:26
- 5 Respostas
- 3496 Exibições
- Última mensagem por Douglasm

Dom Set 19, 2010 09:44
Álgebra Elementar
-
- equação do 2ºgrau
por malcionio » Dom Jun 24, 2012 11:29
- 3 Respostas
- 2355 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 18:46
Sistemas de Equações
-
- Finalizando uma Eq do 2ºGrau
por leticiamarinho_ » Dom Mar 13, 2011 14:16
- 7 Respostas
- 4094 Exibições
- Última mensagem por LuizAquino

Seg Mar 14, 2011 14:30
Álgebra Elementar
-
- [Funções] Achar a intersecção da parábola 2ºgrau
por thoamas343 » Ter Mar 21, 2017 18:42
- 1 Respostas
- 3080 Exibições
- Última mensagem por petras

Qui Mar 23, 2017 18:28
Funções
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7714 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![z = - (8-5i) \frac{+}{} [\right]\sqrt[]{(8 - 5i)^{2} - (4).(1).(-20)}\left] / 2 z = - (8-5i) \frac{+}{} [\right]\sqrt[]{(8 - 5i)^{2} - (4).(1).(-20)}\left] / 2](/latexrender/pictures/b0f1b1348627677628aa3c7c567a658e.png)
![z= \frac{-8 + 5i}{2} \frac{+}{} \sqrt[]{\frac{89}{4}+ 20i} z= \frac{-8 + 5i}{2} \frac{+}{} \sqrt[]{\frac{89}{4}+ 20i}](/latexrender/pictures/f0f99bacf59763c64689d40d3d13b5c8.png)
![{\left( \sqrt[]{\frac{89}{4}+ 20i} \right)}^{\frac{1}{2}} {\left( \sqrt[]{\frac{89}{4}+ 20i} \right)}^{\frac{1}{2}}](/latexrender/pictures/e3dcc87e1ad33de9e15a06f745c4c6fb.png)
![z = \frac{89}{4}+ 20i ; n=2 ; \left|r \right| = 895 >>\left|r \right|= \sqrt[]{{x}^{2} + {y}^{2}} z = \frac{89}{4}+ 20i ; n=2 ; \left|r \right| = 895 >>\left|r \right|= \sqrt[]{{x}^{2} + {y}^{2}}](/latexrender/pictures/fb5a9b39ab9a932499cfbfacd8d8deb2.png)
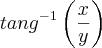 , soh lembrando que z = x + iy
, soh lembrando que z = x + iy



 , avisa que eu resolvo.
, avisa que eu resolvo.

