No desenvolvimento do binômio (ax+by)^5, os coeficientes dos monômios x^2y^3 e xy^4 são, respectivamente, iguais a 720 e 240. A respeito do desenvolvimento desse binômio segundo potências descrescentes de x, sendo "a" e "b" números reais, assinale o que for correto:
(01) a+b=05
(02) "a" é um número ímpar.
(04) O ultimo termo do desenvolvimento é 32y^5
(08) O segundo termo do desenvolvimento é 810x^4.y
(16) O primeiro termo do desenvolvimento é 243x^5


 .
.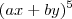 , de forma que temos de substituir na fórmula acima o
, de forma que temos de substituir na fórmula acima o  por
por 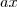 , o
, o  por
por  e tomar
e tomar  . Assim,
. Assim,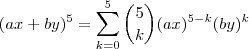 .
.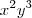 temos de ter
temos de ter  , pois o expoente de
, pois o expoente de  que tem de ser
que tem de ser  ao tempo de que o expoente de
ao tempo de que o expoente de  que é
que é  . Assim, para k=3, temos que o coeficiente de
. Assim, para k=3, temos que o coeficiente de 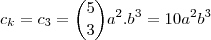
 .
. basta tomar o mesmo raciocínio. Encontramos
basta tomar o mesmo raciocínio. Encontramos  . Assim,
. Assim, 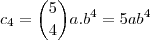 ,
,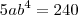 . Portanto, temos duas relações para
. Portanto, temos duas relações para  e
e  :
:
 .
.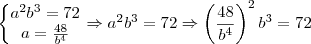
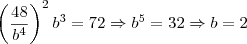
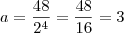 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.