-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 484412 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 546509 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 510324 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 741773 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2193507 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Jhonatan » Dom Out 30, 2016 10:55
por Jhonatan » Dom Out 30, 2016 10:55
A soma (30) + 2(30) + (30) é igual a :
_______(8)____(9)___(10)
R: (32)
__(10)
Pessoal, estou começando agora com Binômio de Newton.
Poderiam me esclarecer como faço para resolver esse modelo de questão ?
Muito obrigado.
-
Jhonatan
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jul 07, 2016 10:24
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Out 30, 2016 22:47
por DanielFerreira » Dom Out 30, 2016 22:47
Olá
Jhonatan, seja bem-vindo!
Inicialmente, devemos expandir o binômio do meio,veja:
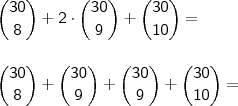
Por conseguinte, aplica-se a
Relação de Stifel:
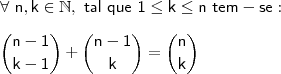
Irei somar os dois termos iniciais... O restante será com você, ok?!
Segue,
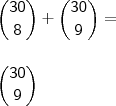
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Jhonatan » Dom Out 30, 2016 23:12
por Jhonatan » Dom Out 30, 2016 23:12
Muito obrigado por sua ajuda, amigo.
Vou tentar terminar aqui.
-
Jhonatan
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Jul 07, 2016 10:24
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Sáb Dez 17, 2016 22:25
por DanielFerreira » Sáb Dez 17, 2016 22:25
DanielFerreira escreveu:Olá
Jhonatan, seja bem-vindo!
Inicialmente, devemos expandir o binômio do meio,veja:
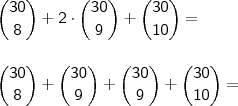
Por conseguinte, aplica-se a
Relação de Stifel:
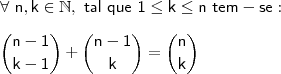
Irei somar os dois termos iniciais... O restante será com você, ok?!
Segue,
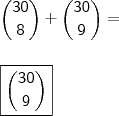
Há um erro na última linha...
O correto seria:

.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Unifor - CE) Função
por gustavoluiss » Dom Jan 30, 2011 20:21
- 2 Respostas
- 3742 Exibições
- Última mensagem por gustavoluiss

Seg Jan 31, 2011 15:53
Funções
-
- (unifor-CE)binomio de newton
por natanskt » Ter Dez 07, 2010 11:38
- 1 Respostas
- 3024 Exibições
- Última mensagem por alexandre32100

Ter Dez 07, 2010 22:25
Binômio de Newton
-
- Simplificação(UNIFOR)-A expressão
por wgf » Seg Mai 27, 2013 20:26
- 4 Respostas
- 8651 Exibições
- Última mensagem por DanielFerreira

Ter Mai 01, 2018 22:54
Álgebra Elementar
-
- função do 1*grau UNIFOR-CE
por Maria Livia » Dom Ago 18, 2013 22:40
- 1 Respostas
- 6481 Exibições
- Última mensagem por Russman

Dom Ago 18, 2013 23:06
Funções
-
- [Múltiplos e divisores]Unifor
por Giudav » Sex Mar 07, 2014 19:48
- 1 Respostas
- 1969 Exibições
- Última mensagem por Russman

Sáb Mar 08, 2014 19:19
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



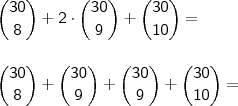
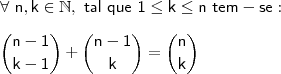
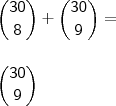


 .
.
