 por andersontricordiano » Qui Jan 26, 2012 14:48
por andersontricordiano » Qui Jan 26, 2012 14:48
Resolva as seguintes equações:
a)

b)
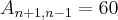
Respostas:
a)S= 6
b)S= 4
Agradeço quem resolver!
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Qui Jan 26, 2012 15:26
por Arkanus Darondra » Qui Jan 26, 2012 15:26
andersontricordiano escreveu:Resolva as seguintes equações:
a)

b)
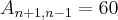
Agradeço quem resolver!
Boa Tarde!
a)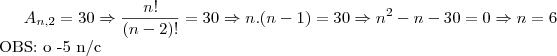 b)
b)![A_{n+1,n-1}=60 \Rightarrow \frac{(n+1)!}{[(n+1)-(n-1)]!}=60 \Rightarrow \frac{(n+1)!}{(n+1-n+1)!}=60 \Rightarrow \frac{(n+1)!}{2!}=60 \Rightarrow (n+1)!=120 \Rightarrow (n+1)! = 5! \Rightarrow n=4 A_{n+1,n-1}=60 \Rightarrow \frac{(n+1)!}{[(n+1)-(n-1)]!}=60 \Rightarrow \frac{(n+1)!}{(n+1-n+1)!}=60 \Rightarrow \frac{(n+1)!}{2!}=60 \Rightarrow (n+1)!=120 \Rightarrow (n+1)! = 5! \Rightarrow n=4](/latexrender/pictures/f48310137a831bc3ba18be4080c08063.png)
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Jan 26, 2012 15:31
por Molina » Qui Jan 26, 2012 15:31
Boa tarde, Anderson.
Vou resolver a primeira e tente fazer a segunda através do mesmo método:
andersontricordiano escreveu:Resolva as seguintes equações:
a)

Sabemos que

Logo,





Encontrando como raízes
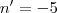
e

Como n não pode ser negativo, ficamos apenas com

Qualquer dúvida informe. Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolva em C, as seguintes equações:
por andersontricordiano » Dom Jan 15, 2012 17:27
- 3 Respostas
- 3092 Exibições
- Última mensagem por fraol

Dom Jan 15, 2012 20:12
Números Complexos
-
- Resolva as seguintes equações:
por andersontricordiano » Seg Jan 23, 2012 12:51
- 2 Respostas
- 1635 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 23, 2012 13:07
Estatística
-
- Resolva as seguintes equações logarítmicas
por andersontricordiano » Seg Set 26, 2011 17:51
- 3 Respostas
- 2956 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 17:21
Logaritmos
-
- (probabilidade) Resolva as seguintes equações
por andersontricordiano » Sex Fev 10, 2012 12:51
- 3 Respostas
- 1997 Exibições
- Última mensagem por MarceloFantini

Sáb Fev 11, 2012 14:44
Estatística
-
- Classifique e resolva , os seguintes sistemas homogêneos.
por andersontricordiano » Ter Jan 03, 2012 23:38
- 1 Respostas
- 3234 Exibições
- Última mensagem por Arkanus Darondra

Qui Jan 05, 2012 00:23
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

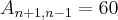


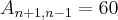

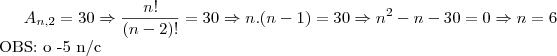
![A_{n+1,n-1}=60 \Rightarrow \frac{(n+1)!}{[(n+1)-(n-1)]!}=60 \Rightarrow \frac{(n+1)!}{(n+1-n+1)!}=60 \Rightarrow \frac{(n+1)!}{2!}=60 \Rightarrow (n+1)!=120 \Rightarrow (n+1)! = 5! \Rightarrow n=4 A_{n+1,n-1}=60 \Rightarrow \frac{(n+1)!}{[(n+1)-(n-1)]!}=60 \Rightarrow \frac{(n+1)!}{(n+1-n+1)!}=60 \Rightarrow \frac{(n+1)!}{2!}=60 \Rightarrow (n+1)!=120 \Rightarrow (n+1)! = 5! \Rightarrow n=4](/latexrender/pictures/f48310137a831bc3ba18be4080c08063.png)







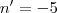 e
e 


