estou com dúvidas na seguinte questão:
"Sabe-se que o conteúdo médio de cerveja numa lata é de 250 ml e variância de 25
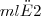 .
. Que percentagem de latas terá menos de 300 ml?
Qual a probabilidade de numa amostra de 6 latas, o conteúdo ser superior a 1.520 ml? "
O primeiro item eu fiz usando obtendo o valor de Z = 10 e portanto a P = 1.
Mas quanto ao segundo item, não sei como calcular a porcentagem a partir da soma do conteúdo das 6 latas,
resolve aplicando naquele curva, com todos os valores multiplicados por 6?
Caso sim, o desvio padrão tbm é multiplicado por 6?
Desde já agradeço!



![\sqrt[]{150} \sqrt[]{150}](/latexrender/pictures/17ec83c6519a2a7a86b43c916f5b170f.png) =12,25.
=12,25.