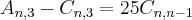
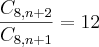
Se alguem puder me ajudar agradeço

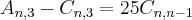
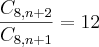

cristina escreveu:Olá estou com duvida neste exercicio.
Se alguem puder me ajudar agradeço
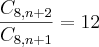
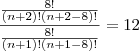 corta 8! de cima com o debaixo fica assim.
corta 8! de cima com o debaixo fica assim. desenvolve (n+2) e (n-6) para poder cortar em baixo.
desenvolve (n+2) e (n-6) para poder cortar em baixo.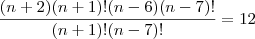 corta (n+1) e (n-7)!
corta (n+1) e (n-7)!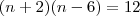 faz a distributiva!
faz a distributiva!
 faz baskara e acha o N!! valeu depois eu resolvo a outra.
faz baskara e acha o N!! valeu depois eu resolvo a outra.

cristina escreveu:Obrigada pela dica, onde é 12 coloquei errado é 2, porém nao consigo achar a raiz quadrada, não dá certo.



cristina escreveu:Oi amigo, já tentei de tudo tbem e não consegui, as alternativas que tenho são:
a) 5
b) 6
c) 1
d) 7
e) 9


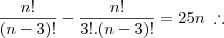




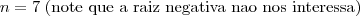
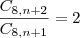


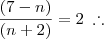
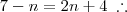


Douglasm escreveu:Bom, vamos ao primeiro: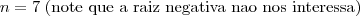
Agora para o segundo problema:
Até a próxima.

cristina escreveu:Obrigada pela dica, onde é 12 coloquei errado é 2, porém nao consigo achar a raiz quadrada, não dá certo.



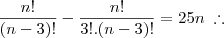


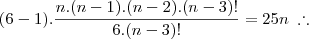



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)