por GMAT2010 » Ter Jan 05, 2010 21:07
Errei esta questão em um simulado que fiz recentemente. Anotei a resposta certa em algum lugar, mas não consigo encontrar mais ela... Gostaria muito que alguém dissesse se encontrei a maneira de resolver ou, caso esteja errado, qual a maneira certa.
O enunciado da questão é: Em um grupo de 20 astronautas, existem 12 com experiência de vôo. Quantos grupos de 3 astronautas podem ser formados, contendo pelo menos uma pessoa com experiência?
A solução que encontrei são 3 combinações. Ou todos os 3 astronautas têm experiência, ou 2 tem e um não tem, ou um tem e dois não tem.
O resultado seria então: C12,3 + C12,2 x 8 + C8,2 x 12
= 12!/(3!(12-3)! + [12!/(2!(12-2)! x 8] + [8!/(2!(8-2)! x 12]
= 220 + 528 + 336 = 1084
Estou certo ou errado?
Muito obrigado pela ajuda
-
GMAT2010
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Ter Jan 05, 2010 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng de Produção
- Andamento: formado
por MarceloFantini » Ter Jan 05, 2010 23:32
Boa noite!
Confesso que não sou muito bom em Análise Combinátoria, mas considerei a questão desta maneira:
Para que tenha
pelo menos um com experiência, é mais fácil pegar todos os grupos de 3 astronautas e retirar os grupos os quais não tem
nenhum com experiência. Logo:
.
Fazendo as contas, cheguei em 1024. É essa a resposta?
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por GMAT2010 » Qua Jan 06, 2010 21:16
Fantini,
Obrigado pela dica. Realmente é mais rápido resolver desta maneira.
Fiz essa conta, e continuo chegando no mesmo resultado: 1084.
Estou errando em algum lugar? Será que realmente é esta a maneira de resolver esta questão?
-
GMAT2010
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Ter Jan 05, 2010 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng de Produção
- Andamento: formado
por MarceloFantini » Qua Jan 06, 2010 22:32
Boa noite!
Cara, desculpe. Sua resposta está certa, errei nas contas.
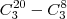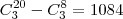, conforme o seu resultado. Foi erro da minha parte!
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador
-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- mediana...não consigo acertar
por TEKA » Seg Mar 29, 2010 11:38
- 1 Respostas
- 3227 Exibições
- Última mensagem por Neperiano
Sex Set 17, 2010 15:36
Estatística
-
- Chance acertar 3 dezenas mega sena
por alezeit » Qui Jan 02, 2014 12:53
- 1 Respostas
- 2823 Exibições
- Última mensagem por Baltuilhe
Dom Jan 21, 2018 03:55
Probabilidade
-
- Preciso de ajuda com essa questão da Fundação Cesgranrio
por Jesicaa » Qui Mar 12, 2015 11:46
- 2 Respostas
- 3010 Exibições
- Última mensagem por Jesicaa
Dom Mar 15, 2015 00:06
Sistemas de Equações
-
- E agora? Dúvida em limites
por Cleyson007 » Sáb Jun 09, 2012 16:24
- 3 Respostas
- 2146 Exibições
- Última mensagem por MarceloFantini
Dom Jun 10, 2012 15:30
Cálculo: Limites, Derivadas e Integrais
-
- Quebrando a cabeça ate agora :/
por Amandatkm » Dom Abr 28, 2013 17:48
- 8 Respostas
- 3959 Exibições
- Última mensagem por Amandatkm
Ter Abr 30, 2013 15:03
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
