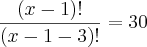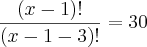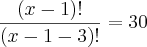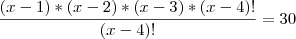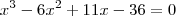por shirata » Qui Nov 26, 2009 06:44
por shirata » Qui Nov 26, 2009 06:44
além dos problemas comuns que normalmente aparecem também existe um tipo de "função combinatória", em que o número de elementos ou agrupamentos é a incógnita. Realmente não faço idéia de como se resolvem esses exercícios, se alguém puder me ajudar, é o seguinte:
- Determine o valor de X, sabendo que:

nesse caso x - 1 é o número de elementos e 3 é o número de agrupamentos. sebendo que se trata de um arranjo, seria algo como:
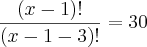
... mas como se resolve isso?
grato desde já...
-
shirata
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 05, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sex Nov 27, 2009 13:49
por Molina » Sex Nov 27, 2009 13:49
Ok. É bem simples. Única coisa que você precisa se lembrar é a definição de fatorial:

Lembre tambem que podemos escrever da seguinte forma:

Então o que você precisa fazer para resolver equações fracionárias envolvendo fatorial é fatoras os termos, de modo que simplifique alguma coisa.
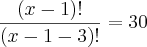

Agora vou fatorar o termo de cima:
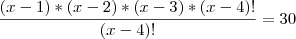
Simplificando...

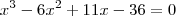
Chegamos nesta equação de terceiro grau que não tem raizes inteiras.
Acho que há algum erro no enunciado. É 30 mesmo? Fiz alguns testes dando valor pra x e nenhum bateu. Mas o importante é você entender o procedimento para fazer outros.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por shirata » Sex Nov 27, 2009 15:00
por shirata » Sex Nov 27, 2009 15:00
não... tranquilo, deu pra entende sim como funciona, valew ae!
-
shirata
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 05, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16353 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12541 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8468 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7921 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6620 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.