- Determine o valor de X, sabendo que:

nesse caso x - 1 é o número de elementos e 3 é o número de agrupamentos. sebendo que se trata de um arranjo, seria algo como:
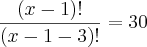
... mas como se resolve isso?
grato desde já...


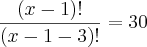



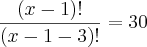

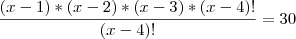

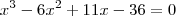



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes