mas vou postar só uma questão.
questão 3.34. A seguinte (de algum modo simplória) previsão de tempo é empregada
por um amador. O tempo, diariamente, é classificado como "seco" ou "úmido ", e
supõe-se que a probabilidade de que qualquer dia dado seja igual ao dia anterior
seja uma constante p (O < p < 1). Com base em registros passados, admite-se que
1 de janeiro tenha probabilidade {B de ser dia "seco". Fazendo {
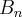= probabilida-de (de que o n-ésimo dia do ano seja "seco"), pede-se obter uma expressão para
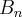em termos de B de p. Calcule também 
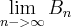interprete o seu resulta-do [Sugestão: Exprima
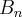termos de 
']minha resolução:
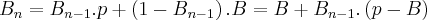
Mas
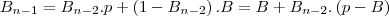
Assim, Por enquanto:
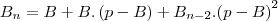
fazendo isso com
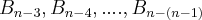, cheguei a seguite expressão:
Porém no gabarito está assim:
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)