tres empresas devem ser contratadas para realizar 4 trabalhos distintos em um condominio.
cada trabalho sara atribuido a uma unica empresa e todas elas devem ser contratadas. de quantas maneiras distintas podem ser distribuidos os trabalhos?
A-12
B-18
C-36
D-72
E-108
eu fiz da seguinte maneira :
4 - número de trabalhos
então
P4 = 4*3*2*1
p4 = 24
ai fiz 3 q é o número de empresas vezes o número de trabalhos:
3* P4 = x
3* 24 = x
x = 72
ai a resposta deu 72 ta certo?
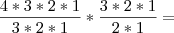
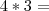
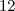
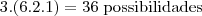
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)