Olá roberoliveira e molina,
Provavelmente há um erro no enunciado, a solução 210 seria para o caso de apenas 1 casal na turma, onde a solução seria a seguinte:
Todas as combinações possíveis dos 11 amigos em grupos de 5 (
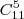
) menos as combinações onde o casal está separado (

, são 2 situações onde eu já selecionei um dos parceiros e faltam 4 vagas a serem preenchidas dentre os amigos restantes, sendo apenas 9 pq não vou selecionar o outro integrante do casal ).
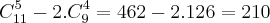
Segui a mesma lógica acima aplicando para 2 casais e também cheguei em 98. Apesar de ser uma solução mais complicada confirma a resposta:
Combinação Completa (
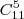
) menos as 4 situações onde apenas 1 membro dentre os 2 casais é chamado (
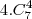
), menos as 4 situações onde 1 membro de cada casal são chamados (
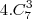
), menos as 4 situações onde 1 casal e mais 1 integrante do outro casal são chamados (

).

E realmente a lógica do amigo do roberoliveira não fez qualquer sentido para mim.





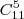 ) menos as combinações onde o casal está separado (
) menos as combinações onde o casal está separado (  , são 2 situações onde eu já selecionei um dos parceiros e faltam 4 vagas a serem preenchidas dentre os amigos restantes, sendo apenas 9 pq não vou selecionar o outro integrante do casal ).
, são 2 situações onde eu já selecionei um dos parceiros e faltam 4 vagas a serem preenchidas dentre os amigos restantes, sendo apenas 9 pq não vou selecionar o outro integrante do casal ).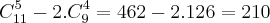
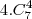 ), menos as 4 situações onde 1 membro de cada casal são chamados (
), menos as 4 situações onde 1 membro de cada casal são chamados (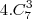 ), menos as 4 situações onde 1 casal e mais 1 integrante do outro casal são chamados (
), menos as 4 situações onde 1 casal e mais 1 integrante do outro casal são chamados ( ).
).