 por roberoliveira » Ter Jun 08, 2010 20:04
por roberoliveira » Ter Jun 08, 2010 20:04
Qual a resposta correta para o problema abaixo, 98 ou 210? Foi-me falado por colegas no curso, que ele é resolvido através de permutações circulares, isso é correto?
Problema:
De quantas maneiras posso convidar 5 amigos de 11, sendo que dentre estes 11 há dois casais cujos membros não podem ser convidados sozinhos.
Alguém poderia me ajudar?
Att, Robert.
-
roberoliveira
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jun 08, 2010 19:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: cursando
 por Molina » Qua Jun 09, 2010 00:00
por Molina » Qua Jun 09, 2010 00:00
Boa noite.
Cheguei como resposta
98 também. Mas gostaria que outra pessoa (ou você mesmo) confirmasse a resposta.
Fiz da seguinte forma:
Dividi em 4 casos:
Caso 1) Ambos os casais não são convidados, restam 5 vagas.
Caso 2) Um dos casais é convidado, restam 3 vagas.
Caso 3) Apenas o outro casal é convidado, restam 3 vagas novamente.
Caso 4) Ambos os casais são convidados, resta 1 vaga.


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por roberoliveira » Qua Jun 09, 2010 20:15
por roberoliveira » Qua Jun 09, 2010 20:15
Boa Noite Molina
Primeiramente muito obrigado pela resolução.
Eu cheguei a C(7,5) + 2*C(7,3) + 7 = 98.
O que me desconcertou neste problema foi o fato de sua resposta ser 210 no livro onde ele aparece (Matemática Discreta, Seymour Lipschutz) e para complicar o amigo que me propôs este problema, o resolveu através de um cálculo estranho* com uso da ideia de permutação circular, que ao meu ver não tem aplicação no contexto desse problema.
* Ele contou cada casal como 1 pessoa (A,B = AB conta como 1 mas continuam sendo 2 pessoas) e usou C9,3 para o caso de um ou dois casais e C9,5 para o caso de nenhum casal. Justificando C9,3 com a fórmula de permutações circulares. Apesar disso não ter uma lógica infálivel ao meu ver**, a soma C9,3 + C9,5 = 210. Enfim acho que tal fato foi uma enorme coincidência, rara de se ver diga-se de passagem.
**Ambas combinações não funcionam em todos casos casos, elas permitem conjuntos ora com mais ora com menos de 5 pessoas.
Att, Robert.
-
roberoliveira
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jun 08, 2010 19:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: cursando
 por angeruzzi » Qui Jun 10, 2010 04:06
por angeruzzi » Qui Jun 10, 2010 04:06
Olá roberoliveira e molina,
Provavelmente há um erro no enunciado, a solução 210 seria para o caso de apenas 1 casal na turma, onde a solução seria a seguinte:
Todas as combinações possíveis dos 11 amigos em grupos de 5 (
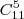
) menos as combinações onde o casal está separado (

, são 2 situações onde eu já selecionei um dos parceiros e faltam 4 vagas a serem preenchidas dentre os amigos restantes, sendo apenas 9 pq não vou selecionar o outro integrante do casal ).
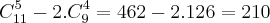
Segui a mesma lógica acima aplicando para 2 casais e também cheguei em 98. Apesar de ser uma solução mais complicada confirma a resposta:
Combinação Completa (
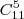
) menos as 4 situações onde apenas 1 membro dentre os 2 casais é chamado (
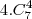
), menos as 4 situações onde 1 membro de cada casal são chamados (
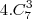
), menos as 4 situações onde 1 casal e mais 1 integrante do outro casal são chamados (

).

E realmente a lógica do amigo do roberoliveira não fez qualquer sentido para mim.
-
angeruzzi
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 16, 2010 00:50
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: formado
 por roberoliveira » Sex Jun 11, 2010 15:27
por roberoliveira » Sex Jun 11, 2010 15:27
Acertou em cheio Angeruzzi, realmente o erro está na interpretação do enunciado cuja forma original é a seguinte:
"Uma mulher tem 11 amigos próximos. De quantas maneiras ela pode convidar cinco deles para jantar, se dois são casados e não comparecem separadamente?"
Foi uma falha de interpretação minha e do meu amigo.
Muito Obrigado.
Att, Robert
Editado pela última vez por
roberoliveira em Sex Jun 11, 2010 16:34, em um total de 2 vezes.
-
roberoliveira
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jun 08, 2010 19:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: cursando
 por angeruzzi » Sex Jun 11, 2010 15:57
por angeruzzi » Sex Jun 11, 2010 15:57
Agora ficou claro roberoliveira, o enunciado diz 2 amigos casados e não 2 casais. Então a minha solução se encaixa no problema.
Desculpe ser chato, mas é que já puxaram minha orelha aqui no fórum, para novas dúvidas abra um novo tópico, as respostas devem ser utilizadas apenas para discussão do problema inicial proposto.
-
angeruzzi
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Mai 16, 2010 00:50
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema de análise combinatória
por Fernanda Lauton » Seg Mar 29, 2010 17:41
- 5 Respostas
- 5737 Exibições
- Última mensagem por Elcioschin

Sex Abr 09, 2010 11:07
Estatística
-
- Problema de análise combinatória
por RJ1572 » Dom Abr 04, 2010 13:28
- 2 Respostas
- 2900 Exibições
- Última mensagem por RJ1572

Dom Abr 04, 2010 21:27
Estatística
-
- [analise combinatoria] problema!
por santtus » Qua Fev 20, 2013 02:18
- 1 Respostas
- 2174 Exibições
- Última mensagem por Rafael16

Qua Fev 20, 2013 11:57
Análise Combinatória
-
- Problema de análise combinatória.
por Sobreira » Seg Set 15, 2014 01:03
- 1 Respostas
- 4461 Exibições
- Última mensagem por DanielFerreira

Dom Set 21, 2014 14:12
Análise Combinatória
-
- Problema de compinação - análise combinatória
por Fernanda Lauton » Seg Abr 05, 2010 18:07
- 1 Respostas
- 2648 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 19:14
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





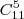 ) menos as combinações onde o casal está separado (
) menos as combinações onde o casal está separado (  , são 2 situações onde eu já selecionei um dos parceiros e faltam 4 vagas a serem preenchidas dentre os amigos restantes, sendo apenas 9 pq não vou selecionar o outro integrante do casal ).
, são 2 situações onde eu já selecionei um dos parceiros e faltam 4 vagas a serem preenchidas dentre os amigos restantes, sendo apenas 9 pq não vou selecionar o outro integrante do casal ).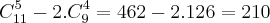
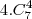 ), menos as 4 situações onde 1 membro de cada casal são chamados (
), menos as 4 situações onde 1 membro de cada casal são chamados (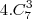 ), menos as 4 situações onde 1 casal e mais 1 integrante do outro casal são chamados (
), menos as 4 situações onde 1 casal e mais 1 integrante do outro casal são chamados ( ).
).


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.