 por acorreia » Qua Abr 18, 2012 18:34
por acorreia » Qua Abr 18, 2012 18:34
Em uma classe de 9 alunos, todos se dão bem, com exceção de Andréia que vive brigando com Manoel e Alberto.
Nessa classe, será constituída uma comissão de 5 alunos, com exigência de cada membro se relacione com todos os outros.
Quantas comissões podem ser formadas ?
GABARITO: 71
Nenhuma sugestão ??
-
acorreia
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qua Abr 18, 2012 18:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por DanielFerreira » Sáb Abr 21, 2012 13:28
por DanielFerreira » Sáb Abr 21, 2012 13:28
Encontrei 41, confirme o bagarito por favor!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Guill » Sáb Abr 21, 2012 13:51
por Guill » Sáb Abr 21, 2012 13:51
.
Editado pela última vez por
Guill em Sáb Abr 21, 2012 20:25, em um total de 2 vezes.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Abr 21, 2012 14:11
por DanielFerreira » Sáb Abr 21, 2012 14:11
Guill,
e quando os três estão na comissão?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por fraol » Sáb Abr 21, 2012 14:46
por fraol » Sáb Abr 21, 2012 14:46
Pessoal, vejam a minha solução:
Podemos ter comissões:
1) Sem a Andréia, então devemos escolher 5 de 8 alunos
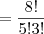
.
2) Com a Andréia, Manoel e Alberto não podem estar na comissão, então devemos escolher 4 de 6 alunos

.
Somando dá 71.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por DanielFerreira » Sáb Abr 21, 2012 16:42
por DanielFerreira » Sáb Abr 21, 2012 16:42
Fraol,
acho que Andréia deveria aparecer em algumas comissões, e entendo que pelas suas contas isso não acontece.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por fraol » Sáb Abr 21, 2012 17:51
por fraol » Sáb Abr 21, 2012 17:51
Oi
danjr5,
No item 2 considero que Andreia está, Manoel e Alberto não.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por DanielFerreira » Sáb Abr 21, 2012 18:04
por DanielFerreira » Sáb Abr 21, 2012 18:04
Ah tá, me desculpe!
Fiz assim:
Se Andréia está na comissão, então a comissão será composta apenas por ela e outros 6, ou seja, total de 7 alunos.

================>

Se andréia não está na comissão, então... 8 alunos.

================>


=
71"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por fraol » Sáb Abr 21, 2012 18:21
por fraol » Sáb Abr 21, 2012 18:21
Fiz assim:
Se Andréia está na comissão, então a comissão será composta apenas por ela e outros 6, ou seja, total de 7 alunos.

================>

Se Andreia estiver na comissão, só poderemos ter outros 4 alunos na comissão, que é de 5. Como Manoel e Alberto não estarão,
só poderemos formar

comissões (6 porque Manoel e Alberto não serão escolhidos, 4 porque Andreia foi fixada em cada comissão).
Se andréia não está na comissão, então... 8 alunos.

================>

.
Ok.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por DanielFerreira » Sáb Abr 21, 2012 20:02
por DanielFerreira » Sáb Abr 21, 2012 20:02
Incrível! Sou tão cego nesse assunto que erro até soma.
rsrss
danjr5 escreveu:21 + 56 = 71
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por marcos chaves » Sáb Abr 21, 2012 22:56
por marcos chaves » Sáb Abr 21, 2012 22:56
Comissão c/ Andreia, significa, sem o portugues e o Alberto
combinações de (9-3) , (5-1) a (5-1) = 6*5/2 = 15
Comissões sem ANDREIA ;Combinações de (9-1) elementos tomados (5 a 5) = (8*7*6)/6 = 56.
Portanto 15 + 56 = 71
-
marcos chaves
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Fev 25, 2012 16:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em matematica
- Andamento: formado
 por acorreia » Ter Abr 24, 2012 17:26
por acorreia » Ter Abr 24, 2012 17:26
marcos chaves, poderia explicar seu raciocínio ?
Até o momento, ao meu entendimento, o raciocínio do Fraol está correto.
-
acorreia
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qua Abr 18, 2012 18:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por Fabiano Vieira » Qui Abr 26, 2012 19:30
por Fabiano Vieira » Qui Abr 26, 2012 19:30
Eu estava analisando essa questão e percebi o seguinte:
Na análise para calcular os grupos formados com Manoel e Alberto, no qual o resultado é 56, teremos grupos com Alberto e Manuel e grupos sem os dois. Assim, para calcular a análise dos grupos possíveis com Andreia, ela necessariamente tem que estar no grupo. Pois se não estiver, os grupos sem ela serão iguais a grupos sem o Manoel e Alberto, ou seja, grupos repetidos.
Temos então:


-
Fabiano Vieira
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Abr 16, 2012 23:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistema de Informação
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16363 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12547 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8471 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7922 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6622 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






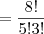 .
. .
.


 ================>
================> 
 ================>
================> 
 = 71
= 71
================>
 comissões (6 porque Manoel e Alberto não serão escolhidos, 4 porque Andreia foi fixada em cada comissão).
comissões (6 porque Manoel e Alberto não serão escolhidos, 4 porque Andreia foi fixada em cada comissão).================>




