Na caixa A existem 12 bombons, dos quais 5 sem recheio.Na caixa B existem 6 bombons dos quais 2 sem recheio.Retirando 1 bombon de cada caixa, qual é a probabilidade de um ter recheio e o outro não?
A partir do enunciado deduzi logo que a ordem pela qual os bombons são retirados das caixas não é relevante.
Primeiro defeni alguns acontecimentos:
A-"Retirar um bombon da caixa A".
Deduz-se que
será retirar um bombom da caixa B.R-"Retirar um bobom com recheio".
Depois escrevi:
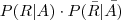
Estas probabilidades refletem as duas situações:
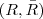e 
.O resultado foi
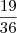.Mas não coincide com o gabarito que é de 
.Depois ainda desenhei uma tabela de dupla entrada.Procedendo depois ao produto/soma:
Os casos favoráveis serão:
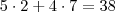
Estou a partir do principio que os casos possiveis são 72.
Onde estou a errar?
, 
por alexandre32100 » Qui Set 09, 2010 21:10
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.