 por gvm » Dom Set 18, 2011 12:45
por gvm » Dom Set 18, 2011 12:45
Olá galera, eu estou vendo essa matéria no cursinho agora e tenho tido alguma dificuldade, resolvi entrar nessa seção pra ver alguns exercícios e algumas resoluções, cheguei ao mesmo valor que o gustavoluiss, abaixo eu coloquei a minha resolução passo a passo, se alguém puder dizer onde eu estou errando ou se é erro no gabarito, eu agradeço.
Desde já obrigado.
Eu particularmente adoto um procedimento bem definido pra resolver esse tipo de exercícios, primeiramente eu defino o conjunto dos números que eu posso utilizar, chamando esse conjunto de A, teríamos:
A = {1,2,4,5,8}
Condição: os números devem ser maiores que 42815.
Assim temos:
1º Caso: o algarismo da dezena de milhar é maior que 4.
Nesse caso existem 2 possibilidades de escolha, o 5 e o 8, portanto:
2 x 4 x 3 x 2 x 1 = 48 possibilidades
2º Caso: o algarismo da dezena de milhar é igual a 4.
Nesse caso o algarismo do milhar deve ser maior que 2, uma vez que o 4 já foi escolhido restam o 5 e o 8, portanto:
1 x 2 x 3 x 2 x 1 = 12 possibilidades
3º Caso: o algarismo da dezena de milhar é igual a 4 e o algarismo do milhar é igual a 2.
Nesse caso o algarismo da centena deve ser maior que 8, o que é impossível uma vez que o 8 é o maior número do conjunto A, portanto:
0 possibilidades
4º Caso: o algarismo da dezena de milhar é igual a 4, o algarismo do milhar é igual a 2 e o algarismo da centena é igual a 8.
Nesse caso o algarismo da dezena deve ser maior que 1, logo podemos escolher o número 5, portanto:
1 x 1 x 1 x 1 x 1 = 1 possibilidade (42851)
Somando dá 61.
Pra conferir fiz ao contrário, calculei o total de permutações possíveis e subtrai aquelas que eram menores que 42815, ficou assim:
1º Caso: o algarismo da dezena de milhar é menor que 4.
Nesse caso podemos ter 1 ou 2, portanto:
2 x 4 x 3 x 2 x 1 = 48
2º Caso: o algarismo da dezena de milhar é igual a 4.
Nesse caso o algarismo do milhar deve ser menor que 2, e portanto igual a 1, assim temos:
1 x 1 x 3 x 2 x 1 = 6 possibilidades
3º Caso: o algarismo da dezena de milhar é igual a 4 e o algarismo do milhar é igual a 2.
Nesse caso o algarismo da centena deve ser menor que 8, podendo ser 1 ou 5, portanto:
1 x 1 x 2 x 2 x 1 = 4 possibilidades
4º Caso: o algarismo da dezena de milhar é igual a 4, o algarismo do milhar é igual a 2 e o algarismo da centena é igual a 8.
Nesse caso o algarismo da dezena deve ser menor que 1, o que é impossível, portanto:
0 possibilidades
Somando tudo da 58, mas eu peguei apenas valores menores do que 42815 e não o próprio 42815, portanto eu devo somar 1 ao resultado final, já que o exercício pede apenas valores maiores do que 42815.
E sendo 5! o total de permutações possíveis, temos que o número de valores maiores do que 42815 é dado por 5! - 59 = 61






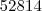 que é maior, ou
que é maior, ou 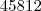 .
.





 .
.
 :
: