por Senhora Duvida » Dom Ago 07, 2011 19:31
Olá!
Minha dúvida é muito básica. Ao ler o problema abaixo e analisar o histograma que vinha junto com ele (arquivo em anexo) a minha resposta foi automáticamente afirmativa para as perguntas. Porém, ao checar a resposta correta, esta dizia que os dados não tem distribuição normal. Eu não consigo entender porque não! Para mim a figura tem formato de sino e é relativamente simétrica. A resposta negativa seria pq ela está deslocada para a direita? Sei que há testes para confirmar se a distribuição é normal, mas neste caso eu não teria todos os dados para calcular...
A quantidade de fósforo foi medida em folhas da espécie fictícia
Arbustus riograndensis. Os dados estão ao lado. Você diria que as
propriedades da curva normal podem ser aqui aplicadas? Por exemplo,
pode-se dizer que aproximadamente 50% dos indivíduos têm valores
abaixo de 8,8? Pode-se dizer que 95% dos valores estão entre
8,8 ± 1,96 (0,21)? Justifique.
Desde já agradeço o auxílio
- Anexos
-
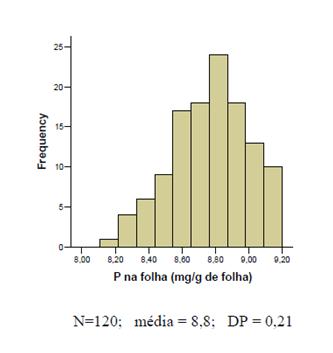
- figura do problema
- histograma.jpg (10.53 KiB) Exibido 1257 vezes
-
Senhora Duvida
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Dom Ago 07, 2011 19:13
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: biologia
- Andamento: cursando
por Neperiano » Dom Ago 07, 2011 21:32
Ola
Você diria que a média está centrada?
Outra coisa, 95% dos elementos estão entre os limites de controle?
Te aconselho a ler a definição de distribuição normal, talvez ajude
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-
Neperiano
- Colaborador Voluntário
-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
por Senhora Duvida » Dom Ago 07, 2011 22:09
Olá!
Obrigada pelos toques!
-
Senhora Duvida
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Dom Ago 07, 2011 19:13
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: biologia
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Distribuição normal] com normal reduzida e tabela, dúvida
por MarciaChiquete » Sáb Set 17, 2016 20:38
- 0 Respostas
- 8250 Exibições
- Última mensagem por MarciaChiquete
Sáb Set 17, 2016 20:38
Estatística
-
- Distribuição normal
por lanahwinchester » Qui Jun 30, 2011 13:58
- 2 Respostas
- 5717 Exibições
- Última mensagem por sena
Sáb Jul 30, 2011 12:41
Estatística
-
- Distribuição Normal
por paivadaniel » Qui Jul 14, 2011 17:23
- 0 Respostas
- 4352 Exibições
- Última mensagem por paivadaniel
Qui Jul 14, 2011 17:23
Estatística
-
- Distribuição Normal
por EulaCarrara » Dom Set 11, 2011 17:05
- 1 Respostas
- 5578 Exibições
- Última mensagem por EulaCarrara
Dom Set 11, 2011 17:19
Estatística
-
- Distribuição Normal
por Jean Almeida » Dom Dez 03, 2017 19:47
- 0 Respostas
- 5686 Exibições
- Última mensagem por Jean Almeida
Dom Dez 03, 2017 19:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
