 por Mppl » Qui Jan 27, 2011 08:11
por Mppl » Qui Jan 27, 2011 08:11
Suponha que a variavel aleatoria X é uniformemente distribuida em [-4; 2]. Sendo
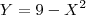
, determine a função densidade de probabilidade de Y .
Bem ate agora eu sei a função de densidade de probabilidade de X=1/6
E tanto quanto sei

se

for positivo ou então
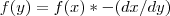
se

for negativo só que tenho um problema com isto... primeiro como parto o intervalo? vou ter que o partir em duas partes so que pelas minhas contas um sobrepoe-se ao outro... e como se não chegasse uma das densidades dá negativa...o que tenho eu mal?
-
Mppl
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jan 26, 2011 21:04
- Formação Escolar: SUPLETIVO
- Área/Curso: Física
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade]Função de variável aleatória bidimensional.
por Bravim » Dom Out 06, 2013 16:57
- 0 Respostas
- 1291 Exibições
- Última mensagem por Bravim

Dom Out 06, 2013 16:57
Probabilidade
-
- Variável Aleatória Exercícios
por snoffao » Ter Nov 25, 2014 16:42
- 0 Respostas
- 2389 Exibições
- Última mensagem por snoffao

Ter Nov 25, 2014 16:42
Probabilidade
-
- Variável Aleatória Exercício 2
por snoffao » Ter Nov 25, 2014 16:46
- 0 Respostas
- 3587 Exibições
- Última mensagem por snoffao

Ter Nov 25, 2014 16:46
Probabilidade
-
- [Probabilidade]Variável Aleatória Contínua
por Bravim » Qui Out 03, 2013 04:56
- 0 Respostas
- 1223 Exibições
- Última mensagem por Bravim

Qui Out 03, 2013 04:56
Probabilidade
-
- Média e variância de uma amostra aleatoria simples c/repsção
por Razoli » Qui Set 17, 2015 10:35
- 0 Respostas
- 1758 Exibições
- Última mensagem por Razoli

Qui Set 17, 2015 10:35
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
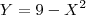 , determine a função densidade de probabilidade de Y .
, determine a função densidade de probabilidade de Y . se
se  for positivo ou então
for positivo ou então 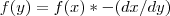 se
se  for negativo só que tenho um problema com isto... primeiro como parto o intervalo? vou ter que o partir em duas partes so que pelas minhas contas um sobrepoe-se ao outro... e como se não chegasse uma das densidades dá negativa...o que tenho eu mal?
for negativo só que tenho um problema com isto... primeiro como parto o intervalo? vou ter que o partir em duas partes so que pelas minhas contas um sobrepoe-se ao outro... e como se não chegasse uma das densidades dá negativa...o que tenho eu mal?


 .
.
 :
: