bolas pretas e três vermelhas. Uma bola é escolhida ao acaso na urna A e colocada na urna B. Uma bola é
então extraída ao acaso, da urna B. Pergunta-se:
(a) Qual a probabilidade de que ambas as bolas sejam da mesma cor?
(b) Qual a probabilidade de que a primeira bola seja vermelha, sabendo-se que a segunda foi preta?
Meu pensamento foi o seguinte, mas não e isso que esta sendo perguntando... Não consigo passar deste ponto...
1ª possibilidade: a bola transferida é vermelha.
Probabilidade de que a bola transferida seja vermelha: P(V) = 1/2 (1 bola vermelha em 2 bolas).
E sorteou vermelha na urna B: P(V/V') = 1/2 * 4/6 = 4/12 (4 bolas vermelhas em 6 bolas)
2ª possibilidade: a bola transferida é preta.
Probabilidade de que a bola transferida seja preta: P(V) = 1/2 (1 bolas preta em 2).
E sorteou preta na urna B: P(V/P) = 1/2 * 3/6 = 3/12 (3 bolas pretas em 6 bolas)
A outra eu nem sei por onde começar
Uma urna X tem 8 bolas pretas e 2 verdes. A urna y tem 4 pretas e 5 verdes e a urna z tem 2 verdes e 7 pretas. Passa-se uma bola de x para y. Feito isto, passa-se uma bola de y para z. A seguir retira-se 2 bolas de z, com reposição. Qual a probabilidade de que ocorram duas bolas verdes.
Se alguem puder me dar um rumo ai, agradeço desde ja


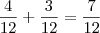 ! Porque nos dois casos são sorteadas duas bolas da mesma cor.
! Porque nos dois casos são sorteadas duas bolas da mesma cor. .
.